<center>阅读:基于风场和海浪同步观测的海浪同化模式构建-王际朝老师博士毕业论文-2014</center>
参考资料
中国知网:基于风场和海浪同步观测的海浪同化模式构建

visio,图片编辑合成;
latex;
致谢
本文是在导师张杰研究员的悉心指导下完成的。感谢导师一路指引我踏入 海洋科学的殿堂。回首四年的求学之路,导师渊博的知识修养和对学术问题的 敏锐洞察力都给我留下了深刻的印象。不仅授我以文,而且教我做人,这将影 响我的一生。在此,我将感激之情化作虔诚的祝福:祝老师身体健康,幸福快 乐。
感谢杨俊钢博士,在国家海洋局第一海洋研究所求学的这几年中,他给我 提供了无私的帮助,并对论文工作给予了建议和指导。感谢杨永增研究员在论 文各个环节中给予的支持和帮助。
特别感谢郭衍游博士和任启峰博士,是他们让我对海浪模式和数据同化方 法的学习少走了很多弯路,本文的工作亦是在两位博士的学位论文的基础之上 完成的,在此表示深深的谢意。
感谢孟俊敏研究员、马毅研究员、纪永刚博士、张晰博士在我求学期间提 供的各种帮助和指导,感谢姚盼盼,庄展鹏,感谢 IDM 组为我提供了良好的学 习环境。
感谢陪伴我打乒乓球的方老师、魏老师和李老师,感谢陪我打篮球的各位 兄弟们,是他们让我的业余生活变的丰富多彩。
感谢父母,感谢妻儿,感谢他们给了我家的温暖,给了我亲情和爱情。
感谢帮助过我的所有人,愿我们能以梦为马,依循自己的梦想前进,愿我们能从现在开始做一个幸福的人,面朝大海,诗酒趁年华。
摘要
海浪数据同化是提高海浪模拟和预报精度的重要途径。影响海浪同化模式精度的四个主要因素为:海浪模式,强迫风场,观测数据以及同化方法。论文基于海浪模式WAVEWATCH III (WW3),从上述四个因素入手,开展了南海、缅因湾和夏威夷三个海域的海浪模拟和同化实验,对海浪模式的三种输入耗散方案进行了评估,研究了同步观测的风场和海浪数据对海浪同化效果的影响机制,研究了基于谱分割策略的EnvisatASAR二维海浪谱最优插值同化。论文的工作可作为中法海洋星CFOSAT卫星应用的预研,对提高我国海浪模拟和预报水平具有实际意义。
论文的第一部分工作是基于HY-2高度计和测波雷达的有效波高数据评估了WW3中提供的三种输入耗散方案,为高质量的海浪模拟提供基础。WW3提供的三种输入耗散方案WAM3,TC96和WAM4都能较好地模拟出海浪的演变趋势,但是在涌浪占主导的情况下,模拟效果均不甚理想。在这些输入耗散方案中,基于‘有效风速’策略的TC96方案的模拟效果最佳,其中的风速校正参数是非常敏感的,为获得高精度的模拟结果,需对此参数进行合理选择。
论文的第二部分工作是以QSCAT/NCEP和CCMP风场为背景风场,通过多组海浪有效波高同化实验,分析了同步观测的风场和海浪数据对同化效果的影响。首先基于NDBC浮标数据,评估了QSCAT/NCEP和CCMP风场,二者精度都较高,2008年3月QSCAT/NCEP和CCMP风速的均方根误差分别为2.93和1.61m/s.然后以这两种风场和融合了浮标风速、风向的风场作为海浪模式的强迫风场,进行了多组海浪同化实验,最后得出结论:既融合观测风场又同化同步获取的海浪数据的同化效果最佳;海浪数据与风场数据在同化效果中所起的作用约为4:1,海浪数据同化能减小海浪模式对强迫风场的高度敏感性。
论文的第三部分工作是基于谱分割策略,实现了Envisat ASAR二维海浪谱数据的最优插值同化,进行了多组模拟和同化实验,比较了有效波高同化与海浪谱同化的同化效果。首先基于NDBC浮标的一维频率谱数据,对2009年至2011年共三年的Envisat ASAR波模式的二维海浪谱数据进行了对比分析。然后对ASAR有效波高、浮标有效波高和ASAR二维海浪谱数据采用不同的同化策略进行了同化实验,最后得出结论:基于谱分割策略的ASAR二维海浪谱同化效果最佳,与仅同化波高相比,均方根误差降低了30%,同化率提高了35%;用于同化的数据源的质量是直接决定同化效果好坏的主要因素之一,浮标的波高同化优于ASAR的波高同化,除了数据质量,待同化数据的观测密度也会对同化效果产生严重影响;虽然ASAR海浪谱的数据质量不如浮标的高,但是ASAR海浪谱同化比浮标波高同化的均方根误差改善了5.6%,同化率提高了17.7%,这是由于二维海浪谱中除了包含表示海浪总能量的有效波高之外,还含有波周期,波传播方向等海浪信息,基于谱分割策略的最优插值同化方法可以用这些信息订正模式背景谱。
关键词:数据同化,同步观测,谱分割,最优插值,WAVEWATCH III
目录


第一章 引言
作为一种重要的海洋现象,海浪与人类的海上活动密切相关。海浪在航海运输、海洋开发、防灾减灾等领域中具有重要地位,而且在海气相互作用和海洋动力环境等研究热点中亦发挥着举足轻重的作用。为研究海浪生成、传播和发展的规律,海浪的数值模拟技术被广泛应用,准确地模拟和预报海浪具有重要的现实意义。多种观测技术手段的发展,使得人们积累了丰富的海浪观测资料,在海浪数值模式发展的基础之上,海浪数据同化成为了提高海浪模拟和预报精度的最有效途径之一。
1.1 海浪预报模式的发展
在二次世界大战时期,由于对海况信息的实际需求,海浪模拟和预报被提上日程。基于对海况的参数化描述以及经验的风浪和涌浪规律,Svedrup and Munk (1947)建立了第一个业务化的海浪预报系统。Pierson et al. (1955) 开创性地提出了海浪谱的概念,但是他们没有给出相应的描述海浪谱发展的动力方程。随后,Gelci et al. (1956,1957)给出了基于谱的能量传输方程,其中描述海浪谱变化率的源函数是从单纯的经验表达式中计算得出的。Phillips (1957)和 Miles (1957)提出了新的风浪生长理论。Hasselmann (1962)导出了源函数的非线性传输方程,并根据新的风浪生长理论把源函数描述为风输入项、非线性能量传输项和‘白冠’引起的耗散项。SWAMP (1985)根据是否考虑非线性相互作用把海浪模式区分为了第一代和第二代海浪模式。第二代海浪模式有两种类型:混合耦合型和离散耦合型。在混合耦合型的模式中,受非线性相互作用控制的风浪谱被假设调整到一个统一的拟均衡形式。与第一代海浪模式类似,由于涌浪不受非线性相互作用的影响,其被认为是一些独立波成分的叠加。线性相互作用的影响,其被认为是一些独立波成分的叠加。虽然加入了非线性相互作用的参数化方案,离散耦合型模式仍利用传统的离散谱的表示形式,这使得其不能更灵活地表示风浪谱以及不能准确地给出一个统一的风浪-涌浪的转换方式。SWAMP 比较了 9 种不同的第一代和第二代海浪模式,发现各种模式的表现是非常不同的。引起这些差别的原因是海浪谱的参数化方案以及谱形状的不同。实际上,与最初假设的参数化海浪谱相比,在海浪模式的积分过程中,海浪谱是非常容易发生变化的,而且海浪谱的二维性比预期的更加重要。因此,第三代海浪模式因此而生。第三代海浪模式中的全谱模式能精确描述海浪发展的物理过程,并且能给出海况的完全的二维描述。
在上世纪 60 年代初期,人们已经建立了海浪预报的理论基础。但是,在当时的海浪模式都不是计算能量平衡方程中的海浪谱。其通常引入一些额外的假设以保证海浪谱遵守预先设定的海浪发展的概念。在能量平衡方程中引入简化的海浪谱是基于两方面的考虑的。一是当时还未认识到波-波非线性相互作用的重要影响,二是当时的计算能力阻碍了能量平衡方程中非线性相互作用的发展。第一代海浪模式发展于上世纪 60 年代和 70 年代初,其假设只要达到一个通用的饱和水平,海浪的所有成分都突然停止发展(Phillips,1958)。饱和谱是由Phillips 的一维 5f 频Phillips 的一维 5 Phillips 的一维 5f 频率谱和经验的均衡方向分布所描述的。目前,通常认为一个通用的高频谱(频率范围为峰值频率的 1.5 至 3 倍)是不存在的,因为谱的高频区域不仅依赖于白冠耗散项和风输入项,而且通过非线性传输,谱的低频部分也对之起到一定的作用。另外,从物理上的观点出发,第一代海浪模式最基本的不足是对风输入源函数项的高估和对非线性传输源函数项的忽略。
在经过大量的海浪生长实验(Mitsuyasu,1968,1969;Hasselmann et al.,1973)和海浪的直接观测(Snyder et al.,1981,Hasselmann et al.,1986)之后,人们发现风输入项和非线性传输项的作用是非常明显的。这就导致了第二代海浪模式的发展。第二代海浪模式尝试解决风输入项的高估现象和海浪谱的高频区域对于低频的依赖。但是,非线性相互作用项的参数化方案非常依赖规定的风浪谱的谱型,事先规定好的风浪谱被强加于能量传输方程的公式中,或者在计算海浪谱时被作为一个边界条件。所以,这些模式在对待风浪和涌浪时遭遇到了基本的问题,而且第二代海浪模式不能很好地模拟出快速变化的风场产生的风浪。
第三代海浪模式中的海浪谱是通过对能量平衡方程进行积分计算得到的,不需要对谱型进行任何限制,并且采用了离散相互作用近似(DIA)来代替第二代海浪模式中对非线性相互作用的简单近似。Snyder et al. (1981) 和 Komen et al. (1984) 提出的输入和耗散源函数项,Hasselmann et al. (1985) 针对非线性相互作用源函数项提出的离散相互作用近似均为为第三代海浪模式提供了较为坚实的理论基础。WAMDI 小组于 1988 年建立了第一个业务化的第三代海浪模式WAM(Wave Model),在其后续的各个版本中,此模式不断地得到改进。在 WAM模式的基础上,袁业立等(Yuan et al.,1991a,b)在控制方程中考虑了浪流相互作用,发展了 LAGFD-WAM 海浪模式;尹宝树等(Yin et al., 1996)在 WAM 模式的框架下提出了 YE-WAM 海浪模式;文圣常等(Wen et al.,1999)基于选定的风浪方向谱,提出了一个建立海浪数值预报模式的新途径。杨永增等(Yang et al., 2000)在 LAGFD-WAM 的基础上,导出了球坐标系下的能量平衡方程,发展了MUSNUM 数值模式;Booij et al. (1999) 考虑浅水效应,发展了适用于近岸区域的海浪模式 SWAN (Simulating Wave Nearshore); Tolman et al. (2002) 基于 WAM模式发展了 WAVEWATCH III (WW3) 模式,NOAA 以 WW3 作为业务化海浪预报模式,对全球及区域海洋进行海浪模拟和预报。目前,第三代海浪模式中,不同的模式采用了不同的物理参数化方案,模式的模拟和预报性能与这些参数化方案密切相关。WW3 模式提供了不同的数值方法和参数化方案以供选择,本文采用 WW3 海浪模式开展相关工作。
1.2 海浪数据同化概述
关于物理过程和计算方法,第三代海浪模式明显地优于第一和第二代海浪模式,但是在自然界中仍然存在一些复杂的情况难以控制,海浪模拟的结果与实际的情况仍然存在偏差。在目前的海浪模式中,采用的都是半经验半理论的方法,以致模式中存在大量的参数化方案,而这些参数化方案是根据经验和观测得到的,在某海域适用的方案不一定适用于其他的海域,这是产生偏差的原因之一。另外一个原因是模式中输入的强迫风场可能与实际的风场相距甚远,以致模式模拟和预报结果不够准确。为获取更高精度的海浪场,人们利用各种观测数据对海浪模式的模拟和预报结果进行改进,这样,就产生了海浪数据同化(Data Assimilation)这一科学问题。
1.2.1 有效波高同化
虽然数据同化在大气模式中的应用在上世纪 50 年代已经开始,但是在海浪模式中进行数据同化是相对较新的课题,直到 80 年代才出现。大气模式产生的高质量的风场以及海洋卫星获取的大量的海浪观测使得数据同化延伸到海浪模式中成为可能。
自 1978 年始,人类发射了 Seasat, Geosat, GFO, ERS-1, ERS-2, ENVISAT, Topex/Poseidon, Jason-1, Jason-2, HY-2 等卫星用于监测全球海洋(蒋兴伟和宋清涛,2010)。这些卫星上都搭载了可以观测海浪有效波高(Significant Wave Height,SWH)的高度计。Komen (1985)首次用 Seasat 卫星的有效波高数据提高了海浪预报精度。国内外很多学者开展了高度计有效波高的同化研究(Lionello et al.,1992; Breivik and Reistad, 1994;Young and Glowacki, 1996; 王跃山和黄润恒,1999; 杨永增,2001; 杨永增等,1999,2001;张志旭等,2003a,b;Greenslade and Young, 2004,2005a,b,c; Pinto et al., 2005; 郭衍游,2006;郭衍游等,2006;万莉颖,2006;王毅和余宙文, 2009; 刘向文等,2012;齐鹏和范秀梅,2013)。但是,有效波高同化只能用海浪的总能量来研究分析海浪谱,缺少海浪的方向等资料,使得其没有足够的信息来纠正海浪模式产生的二维谱。
1.2.2 海浪谱同化
相对于有效波高,二维海浪谱中包含了诸如有效波高、波长、波周期、海浪传播方向等海浪特征参数信息(管长龙,2000)。一般情况下,在海浪模式中同化二维全谱(full spectrum)是不实际的。主要的原因是:计算和分析所有的谱成分(spectra components)带来的困难以及其所带来的高计算量。而且,谱成分之间的相关性是存在的,这些相关性非常难定义且会进一步增大计算量。已经提出了很多策略来同化谱。其中一些方法比较简单,通过调整全谱以适应分析波高(Esteva 1988,Bauer 1992),一些方法把风浪和涌浪部分分离出来(Thomas 1988,Foreman 1994, Francis 1990). Lionello (1992) 把谱分类为风浪、涌浪和混合浪,进而针对不同的部分应用不同的技巧把背景谱调整至与同化的均值参数一致。
到 90 年代中期,同化分割的海浪谱数据的思想被提出(Voorrips 1997, Hasselmann, 1997)。 这个思想不是用局地风的特征把谱分割成风浪和涌浪,他们基于谱地形(topography of the spectrum)提出了一种更高级的谱分割(Spectra Partition)的策略,这种方法可以识别出所有存在的波列(wave trains)成分(允许出现多于一个的涌浪波列),进而把每一个分割识别为不同的具有唯一的气象起源的波列,这样,每一个分割就是不相关的。进而,就可以计算出每一个分割的均值积分波参数,而且可以独立地调整每一个分割。
Hasselmann et al. (1997) 基于谱分割策略,将 ERS-1 SAR 图像反演得到的海浪谱同化到 WAM 模式中,改进了谱的某些平均波参数。Voorrips (1997)把 WAM模式应用在北海海域,同化了 pitch-and-roll 浮标谱。同化框架为最优插值,每一个分割在能量上被‘缩放(scaled)’而且在波频率和传播方向上被‘移动(shifted)’以获得分割的分析能量、均值频率和方向。杨永增和张杰(1998)进行了 SAR 海浪谱资料的理想同化研究;Greenslade (2001)在研究澳大利亚的西海岸的海况时发现,尤其是在涌浪占主导的海况条件下,同化海浪谱能改善模式的执行效果;Sannasiraj et al. (2006) 在北海的涌浪建模中尝试使用观测的谱数据,他们认为同化海浪谱具有令人鼓舞的优势;Aouf et al. (2006 a, b, 2008) 在海浪模式 WAM中同化了合成的海浪谱数据,为 SWIMSAT 卫星任务进行了预研;Siddons (2009) 在 SWAN 模式中同化了英格兰东岸的 OSCR (海浪表面流雷达) 的有效波高和均值周期数据。他测试了三种不同的同化策略:3D-VAR,EnOI 和 EnKF。结果表明,对于 3D-VAR 和 EnOI 结果有改善,但是对于 EnKF,结果却不一致。Siddons(2009)认为合并空间相关误差以及移除偏差能提高同化策略的执行效果,在进行同化之前需要对 HF 雷达数据进行严格的质量控制。Portilla(2009)在 WAM 的近岸版本中同化了一个浮标的海浪谱数据,并且基于最优插值调查了产生增益矩阵的不同方法,讨论了同化分割谱的步骤,并且认为这种应用的主要的任务就是如何对交叉-分配(cross-assignment)策略进行高效的描述。Feng et al. (2012) 利用台湾沿海的浮标海浪谱,在台风情况下开展了东中国海的SWAN 模式同化实验;Jennifer et al. (2013) 在 WW3 模式中同化了高频雷达海浪谱数据。2007 年中法卫星合作项目启动,计划于 2015 年在中国发射的中法卫星 CFOSAT 上将搭载可获取海浪谱数据的海浪波谱仪 SWIM(储小青,2011)。海浪波谱仪可提供大面积、长时间序列的全球海浪谱信息,这为海浪谱的同化提供了数据保障。分析表明,同化分割的海浪谱数据是可行的,同化分割的海浪谱数据比同化全谱的均值波参数,在物理和实际应用上都有优势。
1.2.3 风场校正
在海浪数据同化中,风场校正被认为是海浪数据同化的另一方面。Lionello(1992)在拟均衡生长条件(quasi-equilibrium growth conditions)下,对成长中的风浪谱应用广义的无量纲的功率定律导出了局部风速。这样,通过海浪数据同化,校正后的风场数据被用于驱动海浪模式,直到读入下一步的风场信息。之所以要用海浪的信息对风场进行校正,很大一部分原因是因为强迫风场的精度太低。
随着大气模式的发展以及卫星遥感技术的进步,通过各种融合手段,人们已经可以获取较高精度的网格化风场数据用于海浪模式的强迫风场。物理上,强迫风场对海浪模式的作用是至关重要的,海浪模式依赖于风场来成功地对海浪场进行建模。Hui et al. (2006) 在 WW3 海浪模式中测试了四种强迫风场数据,模式的输出结果对强迫风场的选择非常敏感,高精度的风场较低精度的风场确实改善了模式输出的有效波高等海浪参数。
目前,已有一些现场和遥感仪器可以获取同步观测的风场和海浪数据。有些浮标可以同步获取风速、风向、波高、波周期、一维海浪谱等信息,卫星高度计可同时得到有效波高和风速,值得一提的是,CFOSAT 上搭载有可观测风场信息的散射计以及可获取海浪谱的波谱仪,这也使得同步获取风场和海浪谱成为可能。若在进行海浪数据同化的同时,考虑同步观测的风场信息,则必能改善模式的输出,提高海浪模式模拟和预报的精度。
1.3 本文的工作及创新点
成熟的同化策略是影响构建高精度的海浪同化模式的几个主要因素。基于上述几个因素的考量,本文利用第三代海浪模式 WW3 进行了南海海域(几乎封闭),缅因湾海域(半封闭)以及夏威夷海域(全开阔)的海浪模拟和同化工作(图 1.1)。
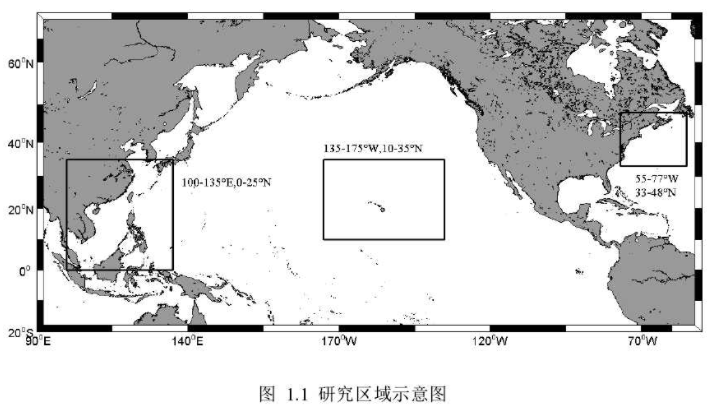
总结起来,论文工作具有以下几个方面的创新性:
- 首次研究了同步观测的风场和海浪数据对海浪同化效果的影响机制;
- 基于 OI-I 同化方法,在海浪模式 WW3 中实现了有效波高数据同化;
- 基于 OI-P 同化方法,实现了 Envisat ASAR 二维海浪谱数据同化。
论文的具体结构为:
- 第一章是引言部分,介绍了海浪数值模式、海浪数据同化的研究进展;
- 第二章介绍了 WW3 模式的源函数项、数值方法和模式结构,以及海浪数据同化方法,并对 OI-I 同化方法进行了详述;
- 第三章基于 HY-2 高度计以及测波雷达的有效波高数据对 WW3 模式中的多种输入耗散方案进行了验证和评估;
- 第四章研究同步观测的风场和海浪数据对同化结果的影响,研究了同步观测的风场和海浪数据的利用策略,基于 OI-I 同化方法,分析了仅同化海浪数据与考虑同步风场观测之后的海浪同化之间的差别;
- 第五章基于 OI-P 同化方法,进行了 Envisat ASAR 二维海浪谱的同化研究,对比分析了波高同化和海浪谱同化的差异,研究了待同化数据的质量对同化效果的影响。
- 第六章对本文的工作进行了总结并给出了展望。
第二章 海浪模式与同化方法
WAVEWATCH III (WW3)是由隶属于美国 NOAA/NCEP 的 MMAB(Marine Modeling and Analysis Branch)开发的全谱空间上的一个第三代海浪模式,目前的最新版本为 3.14. 它是在荷兰代尔夫特理工大学开发的 WAVEWATCH I 和 NASA 戈达德空间飞行中心(Goddard Space Flight Center)研制的 WAVEWATCH II 的基础上,对控制方程、程序结构以及数值和物理的处理方法上都进行了改进(Tolman, 2009)。
对本章以及后续章节中用到的变量声明如下:

2.1 控制方程
在 WW3 模式中,基本的谱是波数方向谱$F(k, \theta)$,模式输出的是常用的频率方向谱 $F(f, \theta)$ 。波数方向谱经过直接的雅克比转换(Jacobian transformation)可得到频率方向谱
$$
F(f, \theta)=\frac{\partial k}{\partial f} F(k, \theta)=\frac{2 \pi}{c_{g}} F(k, \theta)
\tag{2.1}
$$
其中,
$$
c_{g}=\frac{\partial \sigma}{\partial k}=n \frac{\sigma}{k}, \tag{2.2} \
$$
$$
n=\frac{1}{2}+\frac{k d}{\sinh 2 k d} . \tag{2.3}
$$
在不考虑流的情况下,波能是个守恒量。如果考虑到流的影响,由于流会对波的平均动能产生作用,则波能不再守恒(Longuet-Higgins and Stewart, 1961,1962)。但是,一般情况下,波作用量$A \equiv E / \sigma$是个守恒量(Whitham, 1965)。所以,在 WW3 模式中,真正参与计算的是由波数-方向谱$F(k, \theta)$转换得到的波作用密度谱$N(k, \theta) \equiv F(k, \theta) / \sigma$。这样,海浪传播的控制方程表示为
$$
\frac{D N}{D t}=\frac{S}{\sigma}
\tag{2.4}
$$
其中 $D/Dt$ 表示全导数, $S$ 表示与海浪谱 $F$ 有关的源(sources)和汇(sinks)的净效应(net effect)。
球坐标下,关于谱 $N(k, \theta ; x, t)$ 的平衡方程可写为
$$
\frac{\partial N}{\partial t}+\frac{1}{\cos \phi} \frac{\partial}{\partial \phi} \dot{\phi} N \cos \theta+\frac{\partial}{\partial \lambda} \dot{\lambda} N+\frac{\partial}{\partial k} \dot{k} N+\frac{\partial}{\partial \theta} \dot{\theta}_{g} N=\frac{S}{\sigma} \tag{2.5}\
$$
$$
\dot{\phi}=\frac{c_{g} \cos \theta+U_{\phi}}{R} \tag{2.6}\
$$
$$
\dot{\lambda}=\frac{c_{g} \sin \theta+U_{\lambda}}{R \cos \phi} \tag{2.7}\
$$
$$
\dot{\theta_{g}}=
\dot{\theta}-\frac{c_{g} \tan \phi \cos \theta}{R} \tag{2.8}
$$
其中, $R$ 是地球半径, $U_{\lambda}$ 和 $U_{\phi}$ 分别是平均海流矢量在经度 $\lambda$ 和纬度 $\phi$ 方向上的分量, $c_g$ 是群速度。
2.2 源函数项
WW3 模式的源函数项包含以下几项
$$
S=S_{\mathrm{ln}}+S_{i n}+S_{n l}+S_{d s}+S_{b o t}+S_{d b}+S_{t r}+S_{s c}+S_{x x} \tag{2.9}
$$
等式右端依次表示为线性输入项$S_{\mathrm{ln}}$(linear input term)、风-浪相互作用项$S_{i n}$(wind-wave interaction term),也称输入项,波-波非线性相互作用项$S_{n l}$ (wave-wave interactions term)、耗散项 $S_{ds}$(dissipation or whitecapping term)、底摩擦项$S_{bot}$ (wave-bottom interaction term),浅水情况下的水深致波浪破碎项$S_{d b}$(depth-induced breaking term),浅水情况下的$S_{t r}$(triad wave-wave interactions term),底散射项 $S_{s c}$(bottom scattering term)和一个自由项 $S_{x x}$。
2.2.1 波-波非线性相互作用项
考虑非线性的波-波相互作用是第三代海浪模式与第二代海浪模式的主要区别。在海浪传播的过程中,各种谱组分(spectral components)之间会进行能量交换。如果考虑所有组分之间的能量交换,则计算会是一个极端繁重的任务,所以需要做一些近似。一般考虑在四个波组分之间产生这种非线性的相互作用,这四个波组分的波数向量用 $\mathrm{k}{1}$ 到 $\mathrm{k}{4}$ 表示。在 WW3 模式中,提供了两种计算此项的方法,一是 DIA(Discrete Interaction Approximation)方法(Hasselmann et al.,1985),一是 WRT(Webb-Resio-Tracy)方法(Webb,1978; Tracy and Resio,1982; Resion and Perrie,1991)。
由于非线性的波-波相互作用导致的波谱在波数 $\mathrm{K1}$ 上的能量变化表示为如下的 Boltzmann 积分表达式
$$
S_{n l}\left(\mathrm{k}_1\right) =D \sigma \iiint G(\mathrm{k}_1,\mathrm{k}_2,\mathrm{k}_3, \mathrm{k}_4) \delta \left(\mathrm{k}_1+\mathrm{k}_2-\mathrm{k}_3-\mathrm{k}_4\right) \delta \left(\sigma_1+\sigma_2-\sigma_3-\sigma_4\right) \\
\times \left[N_1 N_3\left(N_4-N_2\right)+N_2 N_4\left(N_3-N_1\right)\right]d \mathrm{k}_2 \mathrm{k}_3 \mathrm{k}_4 \tag{2.10}
$$
其中,$G$ 为 Herterich and Hasselmann(1980)给出的复杂的耦合系数,$N$ 为根据波数向量定义的波作用谱密度 $N=N(\mathrm{k})$ 。浅水因子 $D$ 表示为
$$
D=1+\frac{c_{1}}{\bar{k} d}\left[1-c_{2} \bar{k} d\right] \exp \left(-c_{3} \bar{k} d\right) \tag{2.11}
$$
$c_{1}=5.5, c_{2}=5 / 6, c_{3}=1.25$,上标’$-$‘表示谱平均。
…
2.2.2 输入和耗散项
由于输入项和耗散项控制着海浪的生长和消亡,这里,把这两项联合在一起进行考虑。WW3 模式提供了三种可供选择的输入/耗散项。
第一种是基于 Snyder et al. (1981) 和 Komen et al. (1984)提供的输入/耗散项,其亦用在了 WAM 模式的 cycle 1-3 中,这里称这种输入/耗散方案为 WAM3。
WAM3 方案的输入项的表达式为…
相应的 WAM3 耗散项为…
第二种是 Tolman and Chalikov (1996)提出的输入/耗散项,这种方案我们称之为 TC96。
TC96 方案的输入项表达式为…
相应的 TC96 耗散项由低频和高频耗散项构成,用下面的线性组合表示…
第三种输入/耗散方案是由 Janssen (1991)提出的输入项和 Bidlot et al. (2005) 从 WAM3 中修改得到的耗散项组成的,这种方案我们称之为 WAM4。
WAM4 输入项的表达式为…
相应的耗散项是由 Komen et al.(1984)的耗散项 $S_{d s}^{WAM4}$、satured-based 项$S_{d s}^{S A T}$和波-湍流相互作用 (wave turbulence interaction) 项 $S_{d s}^{TURB}$ (Ardhuin and Jenkins ,2006)构成…
2.2.3 线性输入项
线性输入项对模式在静态条件下的快速启动(spin-up)是非常有用的,并且可以改善初始的海浪生长趋势。在 WW3 中,此项的参数化方案采用 Cavaleri and Malanotte-Rizzoli(1981)提出的公式,并联合了 Tolman(1992)给出的一个低通滤波。线性输入项的表达式为…
2.2.4 底摩擦项
底摩擦项采用经验的、线性的 JONSWAP 参数化方案(Hasselmann et al., 1973),表达式为…
2.3 模式特点
WW3 模式的控制方程中包括了因平均水深和平均流场(潮、巨涌等)的时空变化而导致的海浪场的折射和变形,也包含了由于非线性相互作用、风应力、耗散和底摩擦等所导致的波浪成长和消衰。在 WW3 模式中,波的传播考虑为线性的,相关的非线性效应则被包含在源函数项中,而且此模式包含了一个完整的非线性相互作用选项。此外,模式对‘Garden Sprinkler’效应也进行了处理。
数值方面,WW3 模式用标准 FORTRAN 90 编写,完全模块化,易于实现并行计算。模式可以采用规则的经纬度网格或者相似笛卡尔网格,同时用一阶精度(一阶迎风格式)和三阶精度(ULTIMATE QUICKEST)的数值方案来描述波浪的传播。用圆周内均分的角度和空间变化的波数网格来离散化海浪谱,其中波数网格的间隔是符合对数分布的
$$
\sigma_{m+1}=X_{\sigma}\sigma_m
\tag{2.39}
$$
其中,$m$表示波数空间上离散的网格,$X_{\sigma}$ 是自由定义的一个常数,在第三代海浪模式中一般取值为 1.1.
2.4 模式结构
WW3 模式主要包含三个预处理程序、一个主程序和三个后处理程序。其中三个预处理程序为 ww3_grid、ww3_strt 和 ww3_prep,三个后处理程序为ww3_outf、ww3_outp 和 ww3_trck,主程序为 ww3_shel。上述程序的功能以及所对应的的输入和输出列表于表 2.1.
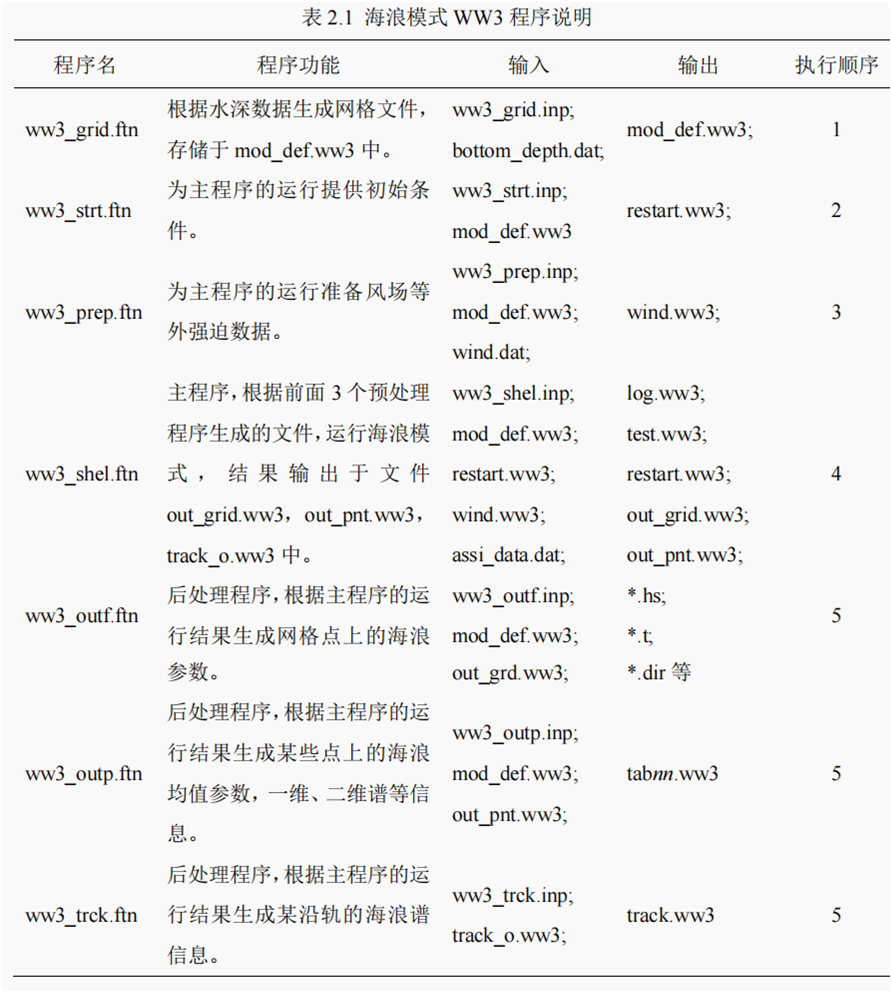
2.5 数据同化方法
所谓数据同化是指根据一定的优化标准和方法,将不同空间、不同时间、不同观测手段获得的数据与数学模型有机结合,纳入统一的分析与预报系统,建立模型与数据相互协调的优化关系,使分析结果的误差达到最小(王跃山,1999)。按照同化方法的理论原理可以分为基于最优控制理论的方法和基于统计估计理论的方法。
基于最优控制理论的方法包括三维变分(Three Dimension VARiation, 3D-VAR)和四维变分(Four Dimension VARiation, 4D-VAR)等方法。变分方法也称为‘多时间水平’(multi-time-level)方法,其在同化过程中用到精确的动力模式,它用一个代价泛函描述模式和观测之间的偏差,进而在各种控制变量下(比如风场,初始条件)极小化这个泛函。
基于统计估计理论的方法包括最优插值(Optimal Interpolation, OI)、卡尔曼滤波(Kalman Filter, KF)、集合卡尔曼滤波 (Ensemble Kalman Filter, EnKF)及其变种等方法(Bishop et al.,2001;Kalnay, 2003; Ott et al., 2004;朱江和汪萍,2006;Harlim and Hunt,2007; Hunt et al.,2007;Reichle et al.,2008;Beezley et al.,2008;Mandel et al.,2010; Miyoshi,2011; Zhu et al., 2011; Sakov et al.,2012;Clayton et al.,2013)。这些基于统计估计理论的方法也称为顺序(Sequential)同化方法或者‘单时间水平’(single-time-level)方法。在实际应用中,顺序同化方法被认为是相对简单并且计算高效的方法。
需要指出的是,在动力模式的线性假设下,KF 方法与 4D-VAR 方法等价,OI 方法与3D-VAR 方法等价(乔方利,2002)。
2.5.1 OI方法的基本原理
OI 方法是一种顺序同化方法,自 60 年代开始就广泛地应用在了大气模式中,其已经被 ECMWF 和 RNMI(荷兰皇家气象学会)用在了业务化的系统中。由于在大气模式应用中的成功,OI 方法被广泛地引入并应用到了海浪模式中(de Valk and Calkoen, 1989; Greenslade, 2001;Hasselmann, et al., 1988, 1997; Hsu, et al., 2011; Komen, 1985;Lionello et al., 1992;Lionello et al., 1995; Siddons et al., 2009; Thomas,1988)。OI 方法历经几十年的发展,在大气和海洋的数据同化中仍然具有非常强的生命力。
最优插值同化方法是使分析误差的方差达到最小的一种统计意义上的线性估计。假设模式的状态变量为$x$,则此状态变量的分析值$x^{a}$由初猜值(或背景值) $x^{f}$ 和观测向量 $y$ 的组合表示为
$$
x^{a}=x^{f}+K\left(y-H x^{f}\right) \tag{2.40} \
$$
$$
K=B H^{T}\left(H B H^{T}+R\right)^{-1} \tag{2.41}\
$$
其中,$H$ 为观测算子,其将背景场的信息转化到观测位置;$K$ 称为增益矩阵,是在极小化分析误差方差的条件下求得的。$B$ 和 $R$ 分别为背景误差协方差矩阵和观测误差协方差矩阵。需要指出的是,在海浪数据同化中,观测变量为有效波高等积分波参数或者海浪谱,不需要转换成其他变量,观测算子 $H$ 只需用于空间插值即可。
2.5.2 误差协方差矩阵
OI 方法的一个最基本的挑战是要制定特定的误差协方差矩阵。
观测误差协方差矩阵
一般情况下,观测误差被认为是空间无关的,这就导致了 $R$ 是一个对角阵,对角线上的元素为观测均方根误差与背景均方根误差的比值
$$
R_{i j}=\delta_{i j}\left(\frac{\sigma_{i}^{o}}{\sigma_{i}^{f}}\right) \tag{2.42}
$$其中 $\sigma_{i}^{o}$ 和 $\sigma_{i}^{f}$ 分别为模式网格点 $i$ 上的观测和背景均方根误差。
背景误差协方差矩阵
为了尽量增大同化策略的优势,必需定义一个空间相关的背景误差协方差矩阵 $B$ 。定义误差的空间相关性是一个繁琐的任务,对 $B$ 的研究一般情况下是转化为对相关函数的分析
$$
B_{i j}=\sigma_{i}^{f} \sigma_{j}^{f} \rho_{i j}
\tag{2.43}
$$这里, $\rho_{i j}$ 为模式网格点 $i$ 和 $j$ 处的背景误差相关函数, $\sigma_{i}^{f}$ 和 $\sigma_{j}^{f}$ 为网格点上 $i$ 和 $j$ 上的的背景均方根误差。表 2.2 列出了背景误差相关函数的多种表达形式。其中,$d_{i j}$ 表示网格点 $i$ 和 $j$ 之间的距离,$L$ 为相关距离尺度(correlation length scale)。
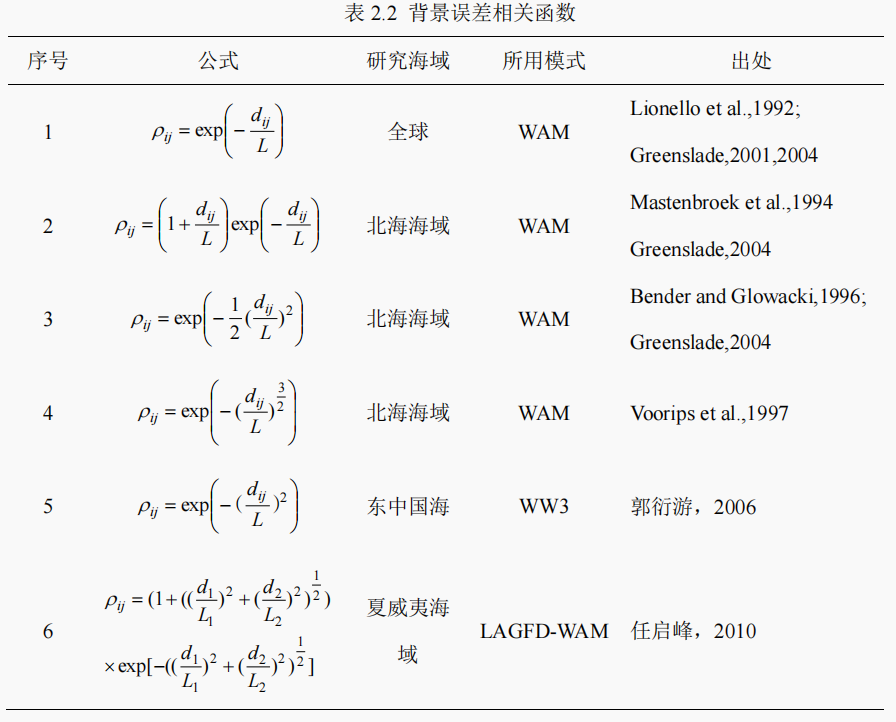
基于 WAM 模式,Greenslade(2004)模拟了 1998 年至 2002 年的全球网格下的海浪场,并与 ERS-2 高度计的有效波高数据进行了比对,详细分析了表中部分误差相关函数。采用表 2.2 中公式 1 至公式 4 所获取的结果差别不大,并且相关距离尺度 $L$ 在高低纬度的值存在明显差别。任启峰(2010)提出了各向异性的背景误差相关函数(表中公式 6),在其进行的夏威夷海域的实验中,背景误差相关函数取为表 2.2 中公式 6 比取为表 2.2 中公式 2 时的同化效果略有改善 (有效波高的均方根误差分别为 0.349m 和 0.354m)。郭衍游(2006)基于 WW3 模式,在东中国海海域进行了有效波高同化实验,其比较了表 2.2 中公式 1 和公式 5 的拟合效果,认为后者比前者略好。基于上述分析,易知采用何种背景相关函数的表达式进行同化,差别不会很大。本文采用表 2.2 中的公式 5 进行有效波高和海浪谱的数据同化研究。需要特别说明的是,表 2.2 各个公式中的相关距离尺度是非常不同的,即使对同一个表达式,$L$ 的取值也具有很大的差异性,比如 Bauer et al.(1992)运用表 2.2 中的公式 1 进行了相关的同化研究,其给出最优相关距离尺度为 1650 km,而在 ECMWF 的业务化预报系统中,运用的是同样的公式,但是相关距离尺度却选择了远小于 1650 km 的 300 km。
2.5.3 OI-I 同化方法
OI 同化策略包含两步。一是,通过对背景和观测进行最优插值,得到有效波高等积分波参数的分析场。二是,基于分析的有效波高更新模式产生的二维海浪谱以得到分析谱,模式把此分析谱当作背景谱进行下一步积分。
由于第三代海浪模式是谱模式,在得到分析的有效波高等积分波参数(Integral wave parameters)后,需要联合背景谱和分析的积分波参数以计算出分析谱。当风浪的能量大于总能量的 3/4 时,二维谱被看作是风浪谱,否则二维谱被看作是涌浪谱。分析的二维谱 $F^{a}(f, \theta)$ 由模式的背景谱 $F^{f}(f, \theta)$ 经过缩放和频移得到
$$
F^{a}(f, \theta) = A F^{f}(Bf, \theta)
\tag{2.44}
$$
针对风浪谱和涌浪谱,参数 $A$ 和 $B$ 有不同的计算方法。
- 当二维谱为风浪谱时,根据 Kitaigorodskii (1962)的理论,公式中的参数 $A$ 和 $B$ 可由经验的风时有限的海浪生长关系、无量纲的能量 $E_{}=u_{}^{4} E / g^{2}$ 、无量纲的均值频率 $f_{m^{}}=u_{} f_{m} / g$ 和无量纲的风时 $T_{}=u_{} T / g$ 得到
$$
A=\left(\frac{h_{s}^{a}}{h_{s}^{f}}\right)^{2}\left(\frac{f_{m}^{f}}{f_{m}^{a}}\right)^{2}
\tag{2.45}
$$
$$
B=\left(\frac{f_{m}^{f}}{f_{m}^{a}}\right)^{2}
\tag{2.46}
$$
- 当二维海浪谱为表现为涌浪时,$A=\left(\frac{h_{s}^{a}}{h_{s}^{f}}\right)^{3/2}$,$B=\left(\frac{h_{s}^{a}}{h_{s}^{f}}\right)^{1/2}$。
基于 WAM 模式,Lionello(1990)指出,在涌浪谱上乘上参数 $A$ 和 $B$ 对背景谱进行缩放和频移并没有产生令人满意的结果。另外,对海浪谱进行风浪和涌浪的区分更增加了计算的复杂度。鉴于此,在进行积分波参数的海浪数据同化时,都不再进行风浪和涌浪的区分,而是统一地采用公式(2.45)和(2.46)。如果仅用分析的有效波高和背景谱来描述分析谱,则分析谱 $F^{a}(f, \theta)$ 可有模式的背景谱 $F^{f}(f, \theta)$ 经过直接经过缩放得到
$$
F^{a}(f, \theta) = \left(\frac{h_{s}^{a}}{h_{s}^{f}}\right)^{2} F^{f}(f, \theta)
\tag{2.47}
$$
这种同化有效波高等全谱的积分波参数的 OI 方法,我们称之为 OI-I 方法。OI-I同化方法只能同化有效波高等积分波参数。这使得此方法有两方面的不足:
- 一是,不可能用这个方法同化一维和二维海浪谱。
- 二是,谱型的详细信息未被考虑,所以在谱型上只能完全依赖于模式的背景谱。
所以,我们需要一个可以同化海浪谱的细节以及方向等信息的新的同化方法。联合 OI 方法,基于谱分割(Spectra Partition)策略的同化方法我们称之为 OI-P 方法,其细节将在第五章中给出。
第三章 输入/耗散源函数项的评估
如前文所述,WW3 的 3.14 版本中提供了 3 种输入耗散方案,称之为 WAM3,TC96 和 WAM4 方案。Tolman(2002)指出,在海浪建模的过程中,考虑表面应力 (surface stresses) 中的浮力效应 (buoyancy effects) 并 不能处理大气层结(atmospheric stratification)带来的影响。
一般情况下,对于大部分海洋来说,大气层结接近于中性(neutral)条件,所以,把模式调整到适合这个条件看起来是比较合理的。但是,Tolman(2002)通过一些测试实验,建议应该把模式调整到适于风区有限增长的不稳定条件(unstable conditions)。为了提高模式的精度,理论上,应该在模式的源函数项中充分考虑大气不稳定性的影响。但是重新调整模式的参数化方案是非常繁琐和复杂的。Tolman (2002)提出了一个简单的方法来重调模式,这个方法是通过在模式内部定义一个所谓的‘有效风速(effective wind speed)’以考虑大气不稳定性的影响。
由于这个策略能保持目前的源函数项的平衡而且明确考虑到了大气不稳定性(atmospheric instability)的影响,这个简洁的方法应用到了 WW3 的 1.15 以及后续版本中。这个‘有效风速’ $u_e$ 被定义为
$$
\frac{u_{e}}{u}=\left(\frac{c_{0}}{1+C_{1}+C_{2}}\right)^{-1 / 2}
\tag{3.1}
$$
$$
C_1=c_1 \tanh [ \max (0, f_1 \{ S T-S T_0 \} ) ]
\tag{3.2}
$$
$$
C_{2}=c_{2} \tanh [\max (0, f_{2} \{S T-S T_{0} \})]
\tag{3.3}
$$
$$
S T=\frac{h g}{u_{h}^{2}} \frac{T_{a}-T_{s}}{T_{0}}
\tag{3.4}
$$
typora显示有误,以网页显示为准;
\left … \right 不能使用;
两个’\‘加上{,才能编译出{ ;
[]不需要加’\‘;
其中 $u$ 为海面 10m 处风速,$ST$ 为稳定性参数,$T_a$ , $T_s$ 和 $T_0$ 是大气、海洋以及基准温度(Tolman 2009)。默认设置中, $c_{0}=1.38, c_{1}=-0.1, c_{2}=0.1, f_{1}=-150, S T_{0}=-0.011, f_{2}=f_{1} c_{1} / c_{2}$ 。其中,$c_0$ 被称为风速校正参数,其在模式的源函数项中是一个非常重要的参数,本文对这个参数的敏感性也进行了分析。其实,这种策略是把大气不稳定性的影响转化成对摩擦速度的影响。
3.1 模式设置
为了测试三种输入耗散方案的模拟能力以及大气稳定性的影响,进行模拟实验。研究区域为南海及其周边海域(如图 3.1)。南海是中国最深、最大的海,其平均水深达到 1212m,最深处达到 5567m。南海是继珊瑚海(Coral Sea)和阿拉伯海(Arabian Sea)之后的第三大陆缘海,并且是一个半封闭的热带海,具有极其复杂的地形。在它的西部和北部是亚洲大陆,东部为菲律宾群岛,印度尼西亚位于南海的南部。
采用嵌套模拟方案,大区域范围为 100-135°E,0-35°N,分辨率是 1/2°×1/2°;小区域范围是 105-122°E,4-25°N,分辨率为 1/6°×1/6°。模式谱被离散为 24 个方向和 25 个频率(0.0412Hz to 0.4056 Hz),初猜谱采用 JONSWAP 谱。风场采用ERA-Interim 的风场数据,其空间分辨率为 1/4°×1/4°,时间分辨率为 6 小时。模式运行的时间为 2012 年 1 月 1 日 0 时至 2012 年 1 月 31 日 18 时。水深数据采用 NOAA 的地球物理数据中心(National Geophysical Data Center,NGDC)提供的 ETOPO-1 数据(Amante and Eakins,2009)。
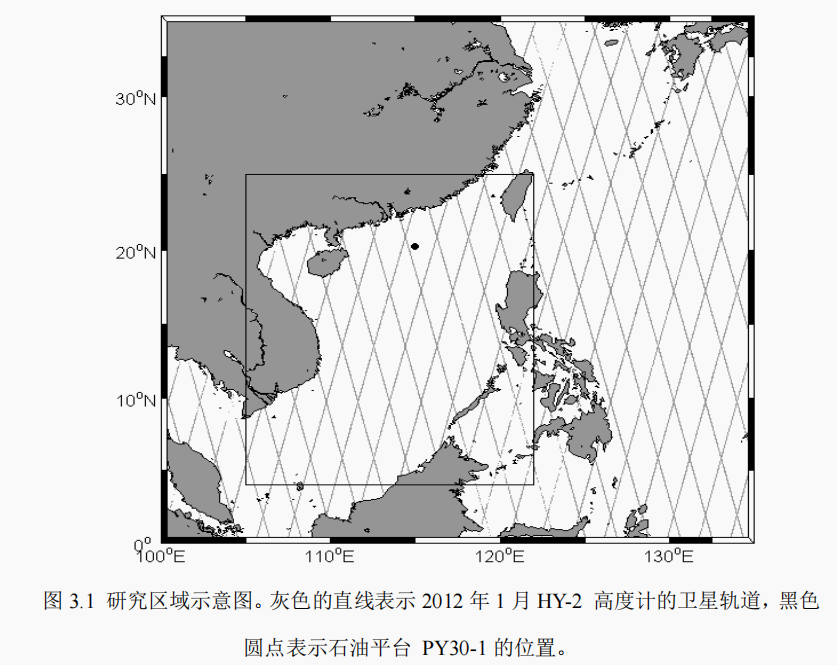
在三种输入耗散项中,考虑大气稳定性的影响,WW3 模式提供了如表 3.1所示的‘开关’以供选择。

开关 ‘STAB2’对应于前文提及的‘有效风速’策略。在 WW3 模式中,WAM4方案中关于是否考虑大气不稳定性影响是通过开关‘STAB3’来控制的。
3.2 验证数据
自 1973 年人类发射了第一颗携带高度计的卫星 SkyLab 以来,为了更好地监测海洋,研究海洋,又陆续发射了几颗携带高度计的卫星。中国于 2011 年 8月发射了 HY-2 卫星,其搭载了雷达高度计、微波散射计、扫描微波辐射计和校正微波辐射计以及 DORIS、双频 GPS 和激光测距仪。以主动微波探测全天候获取海面风场、海面高度和海温为主,满足海洋资源探测、海洋动力环境预报、海洋灾害预警报和国家安全保障系统的要求。HY-2 卫星轨道高度 971 km,轨道倾角 99.34°,是目前世界上唯一在轨运行的集多个微波遥感载荷于一体,具备多要素海洋动力环境观测的海洋遥感卫星,实现了全球海浪、风场、海面高度、海面温度等海面动力环境要素的全天候、全天时、大面积的连续观测。
这里,用国家海洋卫星应用中心(National Satellite Ocean Application Service, NSOAS)提供的 HY-2 高度计的二级产品数据来评估模式在不同源项下的模拟结果。高度计每个 pass 大约跨域 50km 的范围,用时不到 1 分钟,每个 pass 能产生 15-18 个独立的观测,(Durrant et al., 2009)指出,为了数据处理的方便性,可以简单地认为这些观测是同时的。在移除了一些异常数据之后,通过平均处理,图 3.1 所示的研究区域内的高度计波高数据中有效数据为 652 个。用这些处理后的高度计波高数据作为模式的验证数据以评估不同源项的模拟能力。关于 HY-2 高度计有效波高的评估可参见 Wang et al. (2013),其通过 110 个 NDBC 浮标有效波高数据以及 Jason-2 高度计数据对 HY-2 的有效波高进行了评估。
另一种用于验证模拟结果的数据为 C 波段测波雷达(wave observation radar ,WOR)数据。在南海,现场观测的结果非常稀少,本文有幸获取了南海石油平台上的测波雷达数据(863 计划,2008AA09A403)。这个石油平台PY30-1(114.941°E ,20.245°N),其上安装的挪威 MIROS 公司的 SM-050MKIII型 C 波段测波雷达是一种直接传感器,通过测量海水微粒的运动速度来计算海浪高度,可以获得精确的海面波高值,有效波高测量的精度可达 0.2m。
3.3 验证指标
选取均值偏差 Bias、最大偏差 Max_bias 和均方根 RMS 来检验海浪模式的模拟能力,指标定义如下:
均值偏差
$$
\text { Bias }=\frac{1}{N} \sum_{i=1}^{N} (A_{i}-B_{i})
\tag{3.5}
$$
最大偏差
$$
\mathrm{Max} \_ \mathrm{bias} =\max (\operatorname{abs} (A_{i}-B_{i}))
\tag{3.6}
$$
均方根误差
$$
\mathrm{RMS}=(\frac{1}{N} \sum_{i=1}^{N} (A_{i}-B_{i})^{2})^{1 / 2}
\tag{3.7}
$$
typora显示有误,以网页显示为准;
\left … \right 不能使用;
两个’\‘加上_,才能编译出_;
其中,$N$ 表示数据数量,$A$ 为测波雷达或者 HY-2 高度计的观测有效波高,$B$ 为 WW3 模拟的有效波高。
3.4 结果分析
在是否考虑大气稳定性的条件下,为了评估输入耗散项的模拟能力,进行了 5 组实验,分别命名为 WAM3_ST1, TC96_ST2, TC_96STAB2, WAM4_ST3 和WAM4_STAB3。基于 WOR 数据,得到的结果见表 3.2 和图 3.2。图和表中给出的为 2012 年 1 月 5 日至 1 月 30 日的数据。

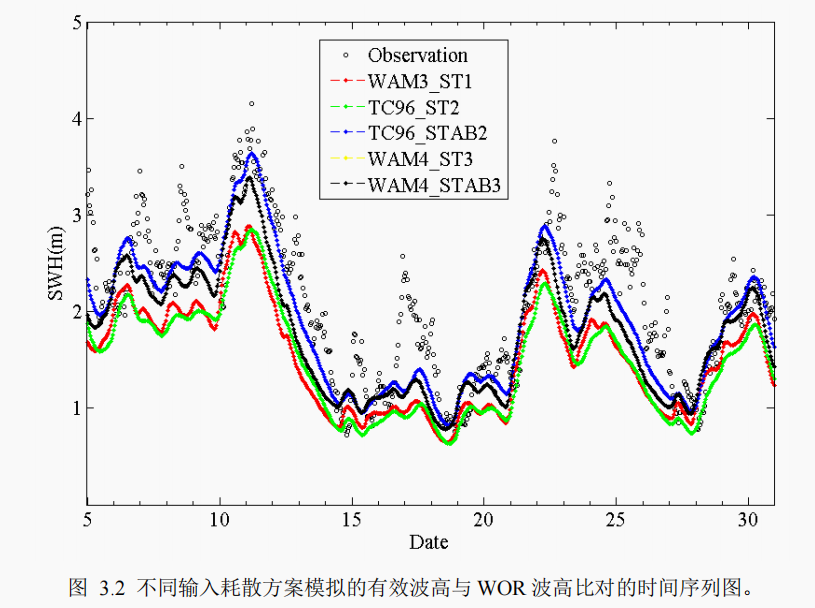
可以得出,TC96_STAB2 的模拟效果最好,即此实验得到的有效波高值最接近 WOR 的实测波高值。WAM4_STAB3的模拟结果仅次之。TC96_ST2 和 WAM3_ST1 模拟的有效波高值比较接近,这也验证了 Georgia et al.(2009)提到的:TC96 的输入耗散项与 WAM3 类似,只是TC96 的耗散函数把谱的低频和高频分成两部分考虑了。所以,图 3.2 中的红色虚线和绿色虚线几乎重合。图 3.2 中绿色虚线和蓝色虚线之间的差别,反映了‘有效风速’策略对模拟结果的影响是非常显著的。
在 WAM4 方案中,大气不稳定性的影响是通过‘STAB3’这个开关控制的。从本文的结果可以看出,实验 WAM4_ST3 和 WAM4_STAB3 的模拟结果几乎没有差别。也就是说,WAM4 方案中的大气不稳定性的影响在 WW3 模式中不能很好地体现出来。这个现象在 Bidlot et al.(2005)把 WAM4 应用到 ECWAM 模式中的时候也出现过,他们发现,是否在 WAM4 方案中考虑大气不稳定性的影响对模拟结果之间的差别影响非常小。Tolman(2009)亦指出,他们正在研究这种差别非常小的原因。所以,在图 3.2 中,黄色的虚线因为黑色虚线的覆盖没有显示出来。同样,基于此原因,表 3.2 中也未列出实验 WAM4_ST3 相关的统计参数。
显然,相比与 WOR 的有效波高数据,采用不同源项的这 5 组实验模拟的波高值看起来都有些偏低。现在,用 ‘最好’的 TC96_STAB2 实验的结果来分析产生这种偏差的原因。在图 3.3 中,蓝色的圈线表示根据风浪关系(WAMDI,1988)计算得到的有效波高值,这里用到的风速是模式的输出数据。
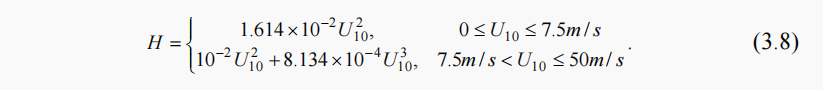
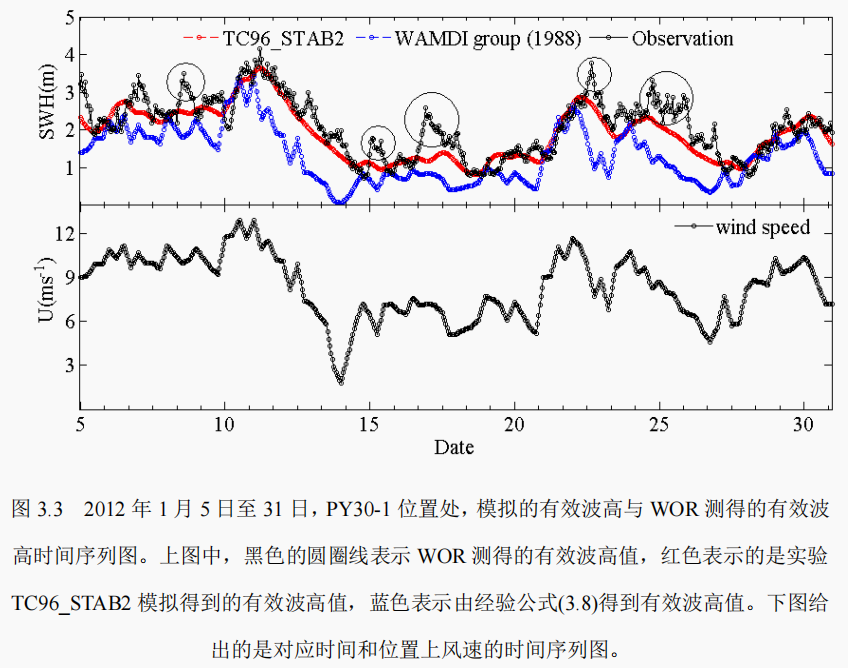
从图 3.3 中可以看出,粗略地讲,模拟的有效波高(红色)与经验公式得到的波高(蓝色)值在趋势上是一致的。图 3.3 中,被大圆围住的点上,模拟的有效波高值相对于当时的风速来说是较大的,这些点上可能受涌浪影响的多一些。显然,在涌浪占主导的时期,上文提及的输入耗散项均不能很好地模拟海浪的消长。这种情况在 Georgia et al. (2009)中也有提及。
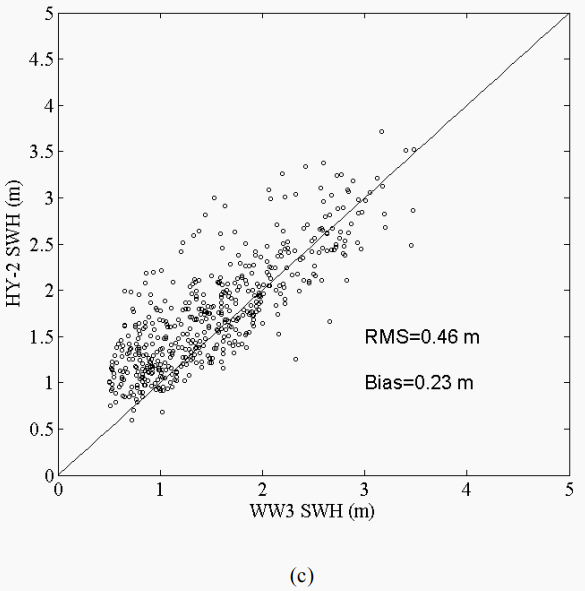
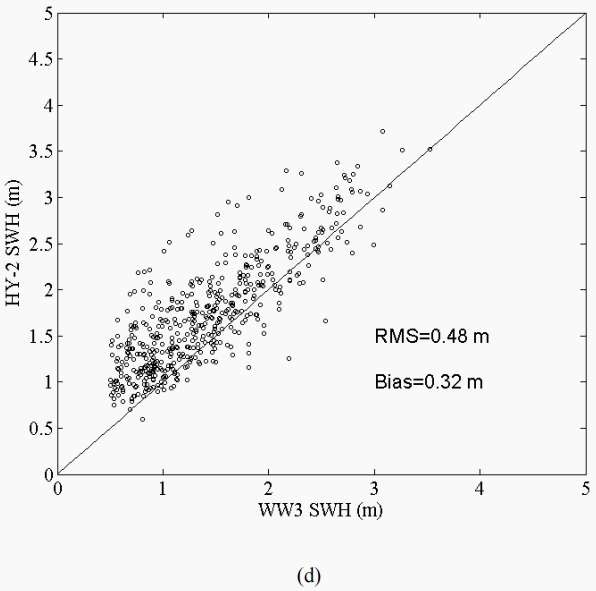
另外,上述五种实验获得的模拟结果还与 HY-2 高度计的有效波高值进行了比较。不失一般性,我们丢弃了那些波高大于 5m 或者小于 0.5m 的点。图 3.4给出了实验 WAM3_ST1,TC96_ST2,TC96_STAB2 和 WAM4_STAB3 的模拟结果与 HY-2 高度计有效波高比对的散点图。模式输出的有效波高与 HY-2 高度计有效波高具有较好的一致性,与和 WOR 比较的结果一致,实验 TC96_STAB2的统计结果最好,其次是实验 WAM4_STAB3 的结果。
 |
 |
 |
 |

3.5 参数敏感性分析
通过与把 5 组实验的模拟有效波高值分别与 WOR 和 HY-2 高度计的有效波高值进行比对,可以得出,在 WW3 模式提供的所有输入耗散项中,用‘有效风速’策略考虑大气不稳定性的 TC96 方案的模拟能力最强。在‘有效风速’策略中,参数 $c_0$ 是非常重要的。Lee et al. (2009) 选择了 8 个最重要的参数进行了敏感性分析,他们得出,在 8 个参数中,公式 (3.1) 中的风速校正参数 $c_0$ 是最重要和最敏感的参数。本文中,对这个参数进行了敏感性分析,并尝试给出此参数在所进行的实验中的最佳值。
对于风速校正参数 $c_0$ ,模式默认值为 $1.38$,在此默认值的一定范围内选择数值进行实验,所选数值为$1.38 \times(1 \pm i \times 10 \%)$,其中 $i$ 是 1,2,3 等。基于 WOR有效波高数据,图 3.5 给出了 $i=\pm 1$ 的情况,也就是选择 $c_0=1.518$ 和 $1.242$ 分别进行类似于 TC96_STAB2 的两组实验。这两组实验的模拟结果与 HY-2 高度计有效波高比对的散点图见图 3.6。


风速校正参数 c0 是非常敏感的,当其取值为 1.518 时,模拟的有效波高值相对于缺省值模拟的有效波高值有一定的改善,但是当其取 1.242 时,模拟结果变的较差。考虑到不同的条件,这个参数的最优值也可能不尽相同,这与风场,水深,研究区域等等都有关系。在本文的实验中,风速校正参数 c0 取比缺省值 1.38 稍大一些的 1.5 可能是一个较好的选择。
总之,WW3 提供的三种输入耗散项都能较好地模拟出海浪的演变趋势。但是在涌浪占主导的情况下,模拟效果均不甚理想。在 WAM3,TC96 和 WAM4这些输入耗散方案中,用‘有效风速’策略考虑了大气不稳定性的 TC96 方案的模拟效果最佳。风速校正参数是非常敏感的,为获得高精度的模拟和预报结果,在某特定区域进行模拟之前,需要对此参数进行验证和选择。
第四章 风场和海浪同步观测的海浪波高同化
风场是影响海浪生长和消亡的重要因素,是海浪预报中的主要误差源之一, 海浪模式也依赖于风场以成功地对海浪进行建模。同时,海浪的数据同化又是 提高海浪模式模拟和预报精度的重要途径。在目前的海浪观测中,有些仪器比如浮标可以获取同步观测的风场和海浪数据,遥感卫星比如 HY-2 上同时搭载的多种传感器亦可同步获取风场和海浪波高数据。即将发射的中法卫星 CFOSAT 上搭载有可获取二维海浪谱数据的海浪波谱仪 SWIM,以及可获取海面风场的散射计 SCAT。这使得同步获取大量的风场和二维海浪谱数据成为可能。可以预见,在进行海浪同化的过程中,充分利用同步观测的风场数据必能进一步提高海浪模拟和预报的精度。本章利用 NDBC 浮标可同步获取风速风向以及海浪波高的能力,研究同步风场的利用策略,分析考虑同步风场后的海浪模拟和同化效果,以在充分利用风场和海浪同步观测信息的前提下建立高精度的海浪同化模式。
4.1 同步风场的数据融合
在海浪数据同化中,风场校正被认为是数据同化的一个重要方面。Lionello(1992) 利用观测的海浪场更新了风场信息。如果初猜谱满足如下条件就被认为是风浪谱,
$$
1.3 \frac{u^{\text {old }}}{c_{p}} \cos \left(\theta_{u}-\theta_{m}\right)>1 \tag{4.1}
$$
其中 $u^{old}$ 是输入的强迫风场的风速,$c_p$ 为海浪谱峰值对应的相速度, $\theta_{u}$ 为风向,$\theta_{m}$ 为均值波向
$$
\theta_{m}=\arctan \left(\frac{\iint F(f, \theta) \sin \theta d f d \theta}{F(f, \theta) \cos \theta d f d \theta}\right)
\tag{4.2}
$$
当上述(4.1)式成立的时候,风速进行如下更新
$$
u^{n e w}=u^{o l d}+u^{a n}-u^{f g}
\tag{4.3}
$$
风速 $u^{an}$ 是从分析的波能 $E^{an}$ 和均值频率 $f_m^{an}$ 中得到的
$$
\frac{g^{2} E^{a n}}{\left(u^{a n}\right)^{4}}=2 \times 10^{-5}\left(\frac{f_{m}^{a n} u^{a n}}{g}\right)^{-2.69}
\tag{4.4}
$$
类似地, $u^{fg}$ 是由初猜的波能 $E^{fg}$ 和均值频率 $f_m^{fg}$ 计算得到。
这样,更新后的风场用作强迫风场驱动海浪模式,直到读入下一步的风场数据。Feng et al. (2012) 对上述方法进行了测试,他们得到的结论是对风场进行 订正远不如对海浪场进行同化,在对模式结果的改善方面,后者对结果改进的 贡献比前者的小的多。注意到,上述方法中,虽然是对风场进行了更新,但是仅仅是针对风速,对于风向却未提及;而且,是使用同化前后海浪的信息更新风场,这会涉及到复杂的风浪耦合机制,按照上述方法更新的风场未必能和下一步输入的强迫风场‘平滑’地衔接在一起。基于业务化预报模式的昂贵的计算代价的考虑,一般不采用此方法对风场进行订正。
在海浪模式中,风场通常只是作为强迫项,在诸多的海浪同化的研究中, 由于风浪耦合机制非常复杂,很少有对风和浪的数据进行联合同化的。de las Heras and Janssen (1992)以及 Bauser et al. (1996) 进行过风浪联合同化的尝试, 相比与单独的海浪有效波高同化,其对海浪的改善效果并不明显。
目前,很多现场和遥感设备可以获取同步观测的风场和海浪信息。NDBC 浮标可以同步获取风速风向和海浪有效波高数据,我国自主研发的遥感卫星 HY-2 上同时搭载的高度计和散射计亦可同步获取风场和海浪波高数据,即将发射的中法卫星 CFOSAT 上亦搭载有可获取二维海浪谱数据的海浪波谱仪和可 获取海面风场的散射计。
为充分利用与海浪场同步观测的风场信息,本文进行如下的操作。首先, 获取较高精度的再分析风场数据,然后把观测的同步风场数据‘融合’到此再分析风场中,得到更高精度的风场,以融合后的再分析风场作为模式的强迫风场驱动海浪模式。由于遥感数据的精度目前情况下还不如浮标的高,虽然空间覆盖率要远远大于浮标的空间覆盖率,但是在区域海洋中可获取的数据不具有时间上的连续性,所以本文用到的同步观测的风场和海浪数据来自与 NDBC 浮标 的风速风向和有效波高。
当然,亦可在大气模式中同化观测的风场数据,得到同化观测风场信息后的大气模式输出的风场,以此风场数据作为海浪模式的强迫风场。这种风场是大气模式输出的直接结果,而再分析风场是在大气模式输出的基础上融合了多 源遥感和现场观测数据的结果,可以预见,同化了同步观测风场数据后的大气模式输出的风场精度应该不如再分析风场的高。
4.1.1 QSCAT/NCEP 和 CCMP 再分析风场
美国大气研究中心(NCAR)提供的 QSCAT/NCEP 的混合风场数据,其空间分辨率为 0.5°x0.5°,时间间隔为 6 小时一次。多平台交叉校正(Cross Calibrated Multi-Platform,CCMP)海面风场数据是 NASA 在 2009 年推出的一种融合了多种卫星遥感平台的新型数据产品,具有较高的时空分辨率,覆盖范围广且具有很高的连续性。该数据集用一种增强的变分同化法融合了 QuikSCAT、 ADEOS-II、AMSR-E、TRMM TMI 和 SSM/I 等诸多海洋被动微波和散射计采集的海面风场数据,具有很高的空间连续性,几乎可以覆盖全球所有海洋(Atlas et al., 2011)。该数据空间分辨率为 0.25°,时间间隔为 6 小时。这两种风场给出的都是距海面 10 m 处风场沿经向和纬向的速度分量。
NDBC 浮标可提供同步的风场和波高数据,为研究同步风场对海浪同化效果的影响机制,本文分别以 QSCAT/NCEP 和 CCMP 再分析风场为背景场,对研究区域内的 10 个浮标的风速和风向进行融合,进而以融合后的风场作为海浪模式的驱动场,进行海浪模拟和同化实验。
我可以也先正常尝试风场的同化~~
图 4.1 给出了研究区域 2008 年 3 月 1 日 6 时 QSCAT/NCEP 和 CCMP 风矢量的 u 分量和 v 分量。图 4.2 展示了这个时间上的两个风场的矢量图。


从两幅图中可以直观地看到,QSCAT/NCEP 和 CCMP 风场数据在量级和空 间结构上既有共性又存在差异。
为了更精确地分析这两种背景风场数据,在进行融合之前,基于 NDBC 浮标的风场数据,先对其进行验证。浮标风速和风向数据为每小时获取一次,其频率高于 QSCAT/NCEP 和 CCMP 再分析风场的每 6 小时一次,将网格化的再分析风场数据插值到浮标位置,便可对这两种再分析风场数据进行验证,由于时间上能完全匹配,时间维度上无需进行插值运算。
采用图 4.3 所列出的 115 个 NDBC 浮标对背景风场进行验证。

图 4.3 中所示的 115 个浮标的经纬度见表 4.1。
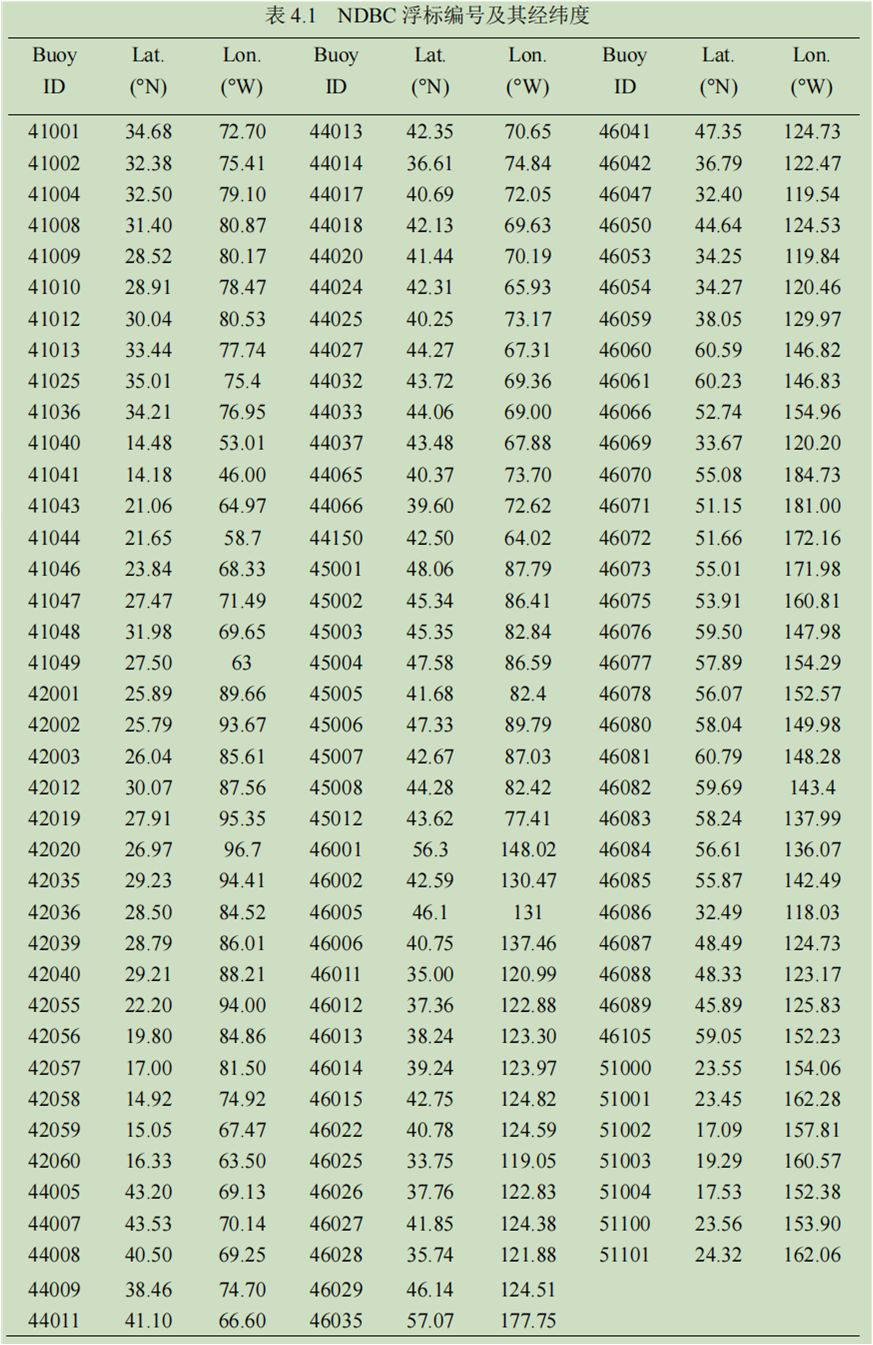
验证指标除了第三章中提及的均值偏差 Bias 和均方根误差 RMS 外,相关系数 Corr 的定义如下
$$
Corr =\frac{\sum_{i=1}^{N}\left(\left(A_{i}-\bar{A}\right)\left(B_{i}-\bar{B}\right)\right)}{\left(\sum_{i=1}^{N}\left(A_{i}-\bar{A}\right)^{2} \sum_{i=1}^{N}\left(B_{i}-\bar{B}\right)^{2}\right)^{1 / 2}}
\tag{4.5}
$$
其中,N 表示数据数量,A 为浮标风速,B 为 QSCAT/NCEP 和 CCMP 风速,横杠为取均值。
以 2008 年 3 月为例,用表 4.1 中列出的 NDBC 浮标的风速和风向对 QSCAT/NCEP 和 CCMP 再分析风场进行验证。共匹配出 7758 对数据, QSCAT/NCEP 风速的均值偏差 Bias 为-0.70m/s, 均方根误差 RMS 为 2.93m/s, 相关系数 Corr 为 0.65。CCMP 风场的 Bias 为-0.54 m/s, RMS 为 1.61 m/s, 相关 系数为 0.91。散点图见图 4.4,这里仅列出 2008 年 3 月的风速散点图,对于 2008年其他月份的风速比较的散点图参看附录 A。从 RMS 等统计参数和图 4.4 都可看出,CCMP 风场的风速精度非常高,QSCAT/NCEP 风场的风速质量相对较差。

对于两种风场的风向数据,仅基于研究区域内的 10 个浮标数据进行了验证。由于风向具有周期性,这会使得一部分数据的验证不太‘公平’,比如浮标风向为 356°,而再分析风向为 6°,若按照正常的计算方式,这两种之间的差距有 350° 之多,但其实二者的差距仅为 10°。因此,为了消除风向的周期性带来的影响, 进行统计时,舍弃了风向小于 10°和大于 350°的浮标和再分析的风向数据。基于研究区域内 10 个浮标风向的统计参数见表 4.2,关于这些匹配数据的风速的统计参数见表 4.3。QSCAT/NCEP 的风向 RMS 为 57°左右,CCMP 的风向 RMS为 33°左右,这说明二者在风向上的差别不如在风速上的差别大。散点图见图 4.5。
RMSE,不太好反应风向再分析数据与真实数据的差异;有什么更好的方法吗?
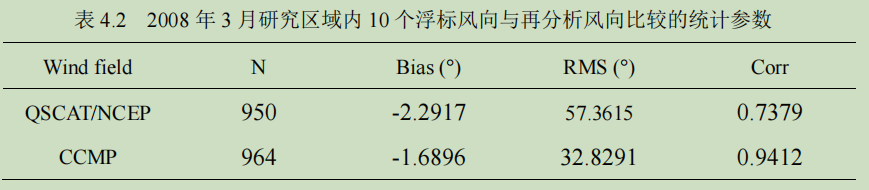


由上可知,QSCAT/NCEP 风场虽然能较好地描述‘真实’的风速和风向,但 其精度不如 CCMP 风场,在后面的海浪模拟和同化实验中,把 QSCAT/NCEP 风场考虑为低精度风场,把 CCMP 风场认为是高精度风场。图 4.6 和 4.7 给出 了浮标 44037 位置处的风速,风向散点图以及相关的统计参数。这里列出的是浮标 44037 位置处的所有有效的风速和风向数据,对于风向并未做前述的‘舍弃’ 处理。
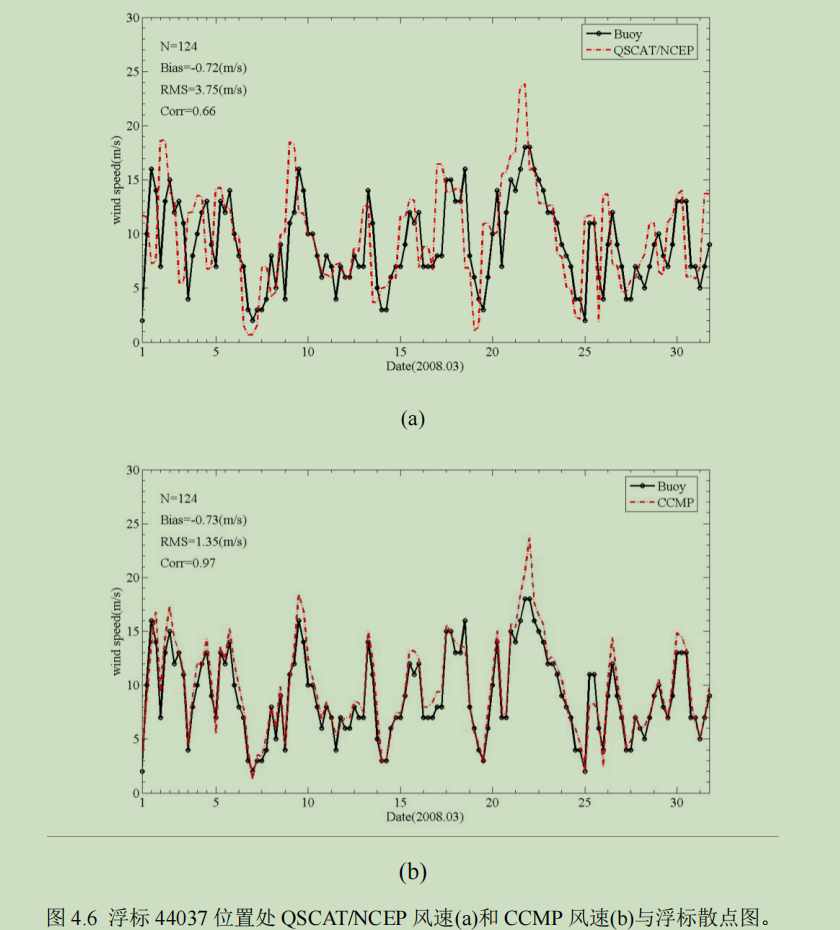

4.1.2 风场数据融合方法
Kako et al. (2011) 基于 NCEP/NCAR 的网格分辨率为 2.5°x2.5°的再分析风 场产品 NRA1(NCEP Reanalysis Average),在经度和纬度方向通过线性插值,得 到了网格大小为 0.25°0.25°的日平均全球风场产品,然后将此 0.25°x0.25°的风 场数据作为背景值,通过最优插值(Optimal Interpolation, OI)算法,对日平均的 ASCAT 风场数据进行了融合,得到高精度的全球 0.25°x0.25°网格风场数据。
本文借鉴此 OI 算法,以网格化的 QSCAT/NCEP 混合风场以及 CCMP 风场作为背景场,融合 NDBC 浮标的风场数据,获取更高精度的风场作为海浪模式的驱动场。
基本公式为
$$
x_{k}^{a}=x_{k}^{f}+\sum_{i=1}^{N}\left(O_{i}-x_{i}^{f}\right) W_{i}
\tag{4.6}
$$
其中,$k$ 为待插值的网格点,$N$ 为此时刻的观测个数,$x_{i}^{f}$ 表示插值到第 $i$ 个观测点位置的背景值,$W_{i}$ 为第 $i$ 个观测点的权重。
这只是对某个网格点进行了同化呀,不是整个区域~~
在假设误差无关(Uncorrelated)和无偏(Unbiased)的情况下,最优的权重 $W_{i}$ 可通过下面的表达式获取
$$
\sum_{j=1}^{N} \sum_{i=1}^{N}\left(\mu_{i j}^{f}+\mu_{i j}^{o} \lambda_{i} \lambda_{j}\right) W_{i}=\mu_{i k}^{f}
\tag{4.7}
$$$\mu_{i j}^{f}$ 为格点 $i$ 与 $j$ 的背景误差相关系数,
$\mu_{i j}^{o}$ 为格点 $i$ 与 $j$ 的观测误差相关系数,
$\lambda$ 为观测均方根误差与背景均方根误差之比
$$
\lambda = \frac{\sigma^o}{\sigma^f}
\tag{4.8}
$$$\lambda$ 一般取值为 1(Kako and Kubota, 2006)。
$\mu_{i j}^{f}$ 由下式得到
$$
\mu_{i j}^{f}=\exp \left(-r_{m}^{2} / L_{m}^{2}-r_{z}^{2} / L_{z}^{2}\right)
\tag{4.9}
$$其中,$r_{z}(r_{m})$ 表示网格点 $i$ 与 $j$ 之间的纬向(径向)距离,$L_{z}(L_{m})$ 为纬向(径向)的相关距离尺度。
与 Kuragano and Shibata (1997) 中提到的 $\mu_{i j}^{o}$ 类似,这里

4.1.3 融合后的风场
基于研究区域内的 10 个浮标的风速和风向数据,通过前文所述的 OI 方法对 QSCAT/NCEP 和 CCMP 风场分别进行融合,相应地,融合后的风场分别记为 NCEP_OI 和 CCMP_OI 风场。表 4.4 中列出了这 10 个浮标的经纬度以及风速的均值、最小值和最大值。

44005,44011,44024 和 44037
4.2 模拟及同化实验
采用 WW3 的 3.14 版本,利用嵌套模拟方案,对缅因湾(Gulf of Maine)海域进行模拟和同化实验(图 4.8)。大区域范围为 55-77°W,33-48°N,分辨率为 0.5°×0.5°,小区域范围为 63-73°W,40-46°N,分辨率为 10min×10min。模拟时间为 2008 年 3 月 1 日 0 时至 2008 年 3 月 31 日 18 时。模式采用的海浪波数谱离散为 24 个波向 (15°分 辨 率 ) 和 25 个波数 , 相应频率范围为 0.04118Hz-0.40561Hz。设置最大全局时间步长为 1500 秒,最大 CFL 条件时间步长 800 秒,最小源函数积分时间步长 30 秒,模拟结果每间隔 1 小时进行一次保存。模式所需的水深数据采用 ETOPO-1 数据。

研究区域内分布有若干 NDBC 浮标,选取表 4.4 中列出的 10 个浮标的风场和波高数据用于风场数据融合及海浪波高同化研究。分别采用 QSCAT/NCEP、 CCMP、NCEP_OI 和 CCMP_OI 风场对海浪模式进行驱动,以分析同步风场对海浪同化效果的影响。本章进行若干模拟和同化实验,同化方法采用第二章中介绍的 OI-I 方法,同化数据为与前文所述的浮标风场同步观测的海浪的有效波高。实验名称及其相关信息见表 4.5.
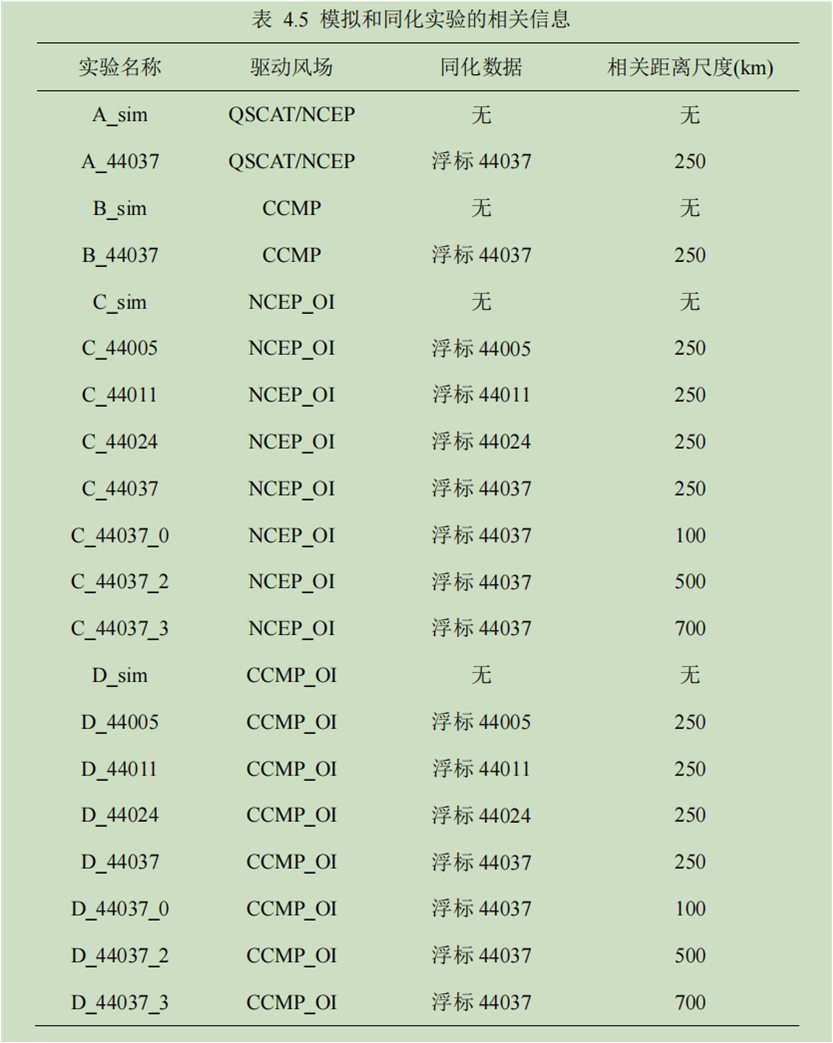
感觉还是只是对点的同化;
选取均值偏差 Bias、均方根误差 RMS、相关系数 Corr 和同化率 AI 来检验海浪模式的模拟能力以及同化效果,前三个指标的定义分别见公式(3.5)、(3.7)和(4.5),关于同化率的定义如下
$$
\mathrm{AI}=\frac{\mathrm{RMSN}-\mathrm{RMSA}}{\mathrm{RMSN}} \times 100 \%
\tag{4.11}
$$
typora显示有误,看博客上的;
其中,RMSN 和 RMSA 分别表示模拟和同化结果相对于浮标真值的均方根误差RMS。
问题:如何同化一个浮标的数据?
4.3 结果分析
对表 4.5 中进行的若干模拟和同化实验,现分别进行分组讨论,以研究风场、海浪数据以及同步观测的风和浪的数据对同化效果的影响,分析同化率与距离的关系,分析不同的相关距离尺度对同化结果的影响。
4.3.1 原始风场驱动的模拟结果
为分析背景风场 QSCAT/NCEP 和 CCMP 作为驱动风场时的海浪模拟的效果,进行了实验 A_sim 和 B_sim。考虑到海浪模式的 spin-up 需要一段时间,舍弃了前 4 天的模拟数据,浮标实测数据和模拟结果之间的比较是从 3 月 5 日 0 时至 3 月 30 日 23 时(下同)。利用 WW3 的‘点输出’功能(ww3_outp),时间间隔 一小时,输出 10 个浮标位置处的有效波高等海浪参数信息。图 4.9 给出了浮标 44005,44011,44024 和 44037 位置处的模拟有效波高对比图,风场精度的不同直接决定了模拟结果的差别。表 4.6 和表 4.7 列出了这两种风场作为模式的驱动风场时,4 个浮标位置处的模拟结果与浮标实测有效波高的统计参数。

看看我的那个10天的模拟,对比一下,吸收经验,我的没有spin-up舍弃数据~~

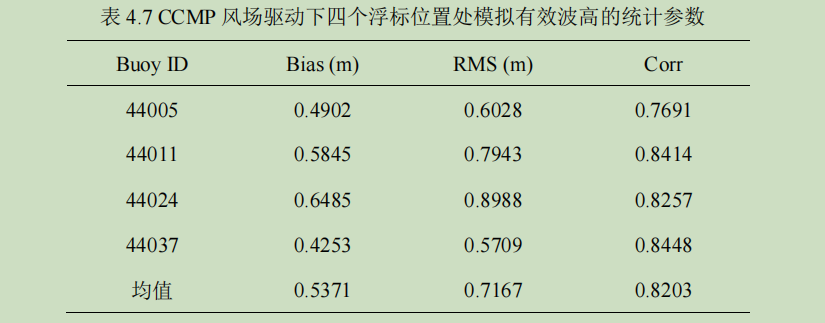
从表 4.6 和 4.7 中可以看出,CCMP 作为驱动风场的模拟结果要比 QSCAT/NCEP 作为驱动风场的模拟结果要好。从均方根误差 RMS 上来看,这两种风场驱动的模拟结果稍有些不理想,但是考虑到这四个浮标点的浮标有效波高均值和最大值(表 4.4),以及浮标实测数据的‘震荡’范围(图 4.9),可以得出, 这两种风场驱动的海浪模式均较好地模拟出了海浪有效波高的变化趋势,作为高精度风场的 CCMP 风场驱动的模拟结果比较低精度的 QSCAT/NCEP 风场驱动的模拟结果要好。这也从侧面反映出驱动风场对海浪模式的重要性。
值得一提的是,由于浮标 44007,44013 和 44033 非常近岸,在目前的水深分辨率和驱动风场分辨率的条件之下,模拟效果比较差,本文不再列出这三个浮标位置处的模拟结果的时间序列图和统计参数。当然,这并不能说明 WW3 没有模拟近岸海浪的能力,Jouon et al.(2009)甚至将 WW3 模式成功地应用与某半封闭的泻湖的海浪建模。另外,限于篇幅,关于浮标 44008,44018 和 44032位置处的模拟结果以及后文中的同化结果见附录 B。
不能说明没有,只是想说不好,Swan~~
4.3.2 融合风场驱动的模拟结果
为分析背景风场 NCEP_OI 和 CCMP_OI 作为驱动风场时的海浪模拟的效果,进行了实验 C_sim 和 D_sim。作为比原始的背景风场更‘精确’的风场数据, 融合了浮标风速和风向的 NCEP_OI 和 CCMP_OI 风场表现的更加出色。以此风场作为驱动风场,在 4 个浮标位置处的海浪有效波高模拟结果见图 4.10,相关 的统计参数见表 4.8 和表 4.9。



正如预期的那样,两种融合风场作为驱动风场的模拟结果比相应的原始背景风场作为驱动风场的模拟结果要好。以浮标 44037 位置处的模拟结果为例, 图 4.11 给出了融合前后的风场作为驱动风场的模拟结果与浮标实测有效波高的对比图。结合四个表 4.6、4.7、4.8 和表 4.9,可以得出,与浮标实测相比,NCEP_OI 驱动的模拟波高比 QSCAT/NCEP 驱动的模拟波高的 RMS 从 0.86m 降为 0.72m, CCMP_OI 驱动的模拟波高比 CCMP 驱动的模拟波高的 RMS 从 0.72m 降为 0.60m. 可见,融合风场作为驱动风场的模拟有效波高 RMS 比原始的背景风场作为驱动风场的模拟有效波高 RMS 降低约 **15%**。当然,这是比较理想的情况, 这个指标跟很多因素都有关系,比如网格化的背景风场的精度、实测风场的精度、实测风场的数据量、实测风场的地理位置分布等。

4.3.3 原始风场驱动与融合风场驱动的同化结果
由上节可以得出,用融合了浮标风速和风向的再分析风场数据作为海浪模式的驱动场,模拟的有效波高精度在 RMS 上有近 15%的改善。本节探求同化与浮标风场数据同步获取的浮标有效波高数据之后,模式输出的海浪参数的改善情况。这里用到的同化方法为第一章中提及的 OI-I 同化方法。进行实验 A_44037,B_44037,C_44037 和 D_44037。实验 A_44037 是指在 QSCAT/NCEP 风场驱动下,同化浮标 44037 的有效波高数据,类似地,实验 B_44037,C_44037 和 D_44037 分别是在 CCMP、NCEP_OI和 CCMP_OI风场驱动下同化浮标 44037 的有效波高数据。
专门针对44037浮标的同化~~
在某个位置同化某个浮标,再用这个浮标验证,这肯定能大幅度提升呀,但貌似用的是其4个浮标验证
嗯嗯
图 4.12 给出了浮标 44005,44011,44024 和 44037 位置处的实验 A_44037 和 C_44037 的同化模拟结果。表 4.10 列出了实验 A_44037 和 C_44037 在上述 4 个浮标位置处与浮标实测波高对比的统计参数。


同样,图4.13给出了浮标44005, 44011,44024 和 44037 位置处的实验 B_44037 和 D_44037 的同化模拟结果。表 4.11 列出了实验 B_44037 和 D_44037 在上述 4 个浮标位置处与浮标实测波高对比的统计参数。


从上述图、表中可以得出,海浪同化大幅度改善了模式的输出结果,四种风场驱动下的海浪模式,在同化了相同的有效波高数据后,模式输出的有效波高值在 Bias、RMS 和 Corr 三个参数上都有较好的表现。以浮标 44011位置处的结果为例,实验 A_44037 的模式输出波高的 RMS 为 0.69m,同化前的 RMS 为 0.85m,RMS 的改善率为 19.7%,实验 C_44037 的模式输出波高的 RMS 为 0.58m,同化前的 RMS 为 0.66m,RMS 的改善率为 12.4%.
需要指出的是,表 4.10 和表 4.11 中的‘均值’指的是在三个浮标(44005, 44011 和44024)位置处的各个统计参数的均值。由于在上述实验中同化的是浮标44037 的有效波高值,所以在浮标 44037 位置处的统计参数只作为参考。
均方根误差 RMS 是一个判断模拟或者同化效果的一个重要指标,联合所述的统计表格,得到了实验 A_sim, B_sim, C_sim, D_sim, A_44037, B_44037, C_44037 和 D_44037 在 4 个浮标位置的 RMS 值(表 4.12)。根据此表格数据,作图 4.14,由于其中的几个实验同化的是浮标 44037 的有效波高数据,所以对于浮标 44037 位置处的 RMS 变化情况在图中没有标出。
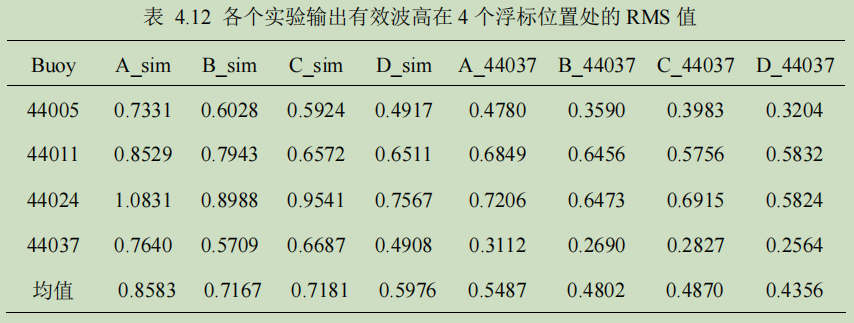

总之,在进行海浪数据同化时,在驱动风场中融合同步观测的风场数据会更加改善海浪同化的效果。下面分两部分对前述实验结果进行统计分析。
以 QSCAT/NCEP 和 NCEP_OI 风场作为驱动风场
仅考虑同步风场的影响,不同化任何海浪数据时(即实验 A_sim 和 C_sim 模 拟结果的对比),模式输出的有效波高的 RMS 降低了 19.2%,22.9%和 11.9%, 平均降低了 18.0%;
仅同化海浪有效波高,不考虑同步风场的影响时(即实验 A_sim 和 A_44037 模拟结果的对比),模式输出的有效波高的 RMS 降低了 34.8%,19.7%和 33.5%, 平均降低了 29.3%;
考虑同步的风场和海浪有效波高数据时(即实验 A_sim 和 C_44037 模拟结果 的对比),模式输出的有效波高的 RMS 降低了 45.7%,32.5%和 36.2%,平均降低了 38.1%.
以 CCMP 和 CCMP_OI 风场作为驱动风场
仅考虑同步风场的影响,不同化任何海浪数据时(即实验 B_sim 和 D_sim 模 拟结果的对比),模式输出的有效波高的 RMS 降低了 18.4%,18.0%和 15.8%, 平均降低了 17.4%;
仅同化海浪有效波高,不考虑同步风场的影响时(即实验 B_sim 和 B_44037 模拟结果的对比),模式输出的有效波高的 RMS 降低了 40.4%,18.7%和 28.0%, 平均降低了 29.0%;
考虑同步的风场和海浪有效波高数据时(即实验 B_sim 和 D_44037 模拟结果 的对比),模式输出的有效波高的 RMS 降低了 46.9%,26.6%和 35.2%,平均降 低了 36.2%
为说明同步观测的风场和海浪数据对海浪同化效果的影响,这里,先给出风场和海浪数据对同化结果的贡献率 RC(Rate of Contribution)的定义。
假设:条件 a 作用于事件 E 上,对 E 的影响为 $\alpha$ ;条件 b 作用于事件 E 上,对 E 的影响为 $\beta$;条件 a 和 b 共同作用于事件 E 上,对 E 的影响为 $\gamma$. 若 $\alpha<\beta<\gamma$,则,条件 b 对事件 E 的贡献率为
$$
R C_{b}=\left|\frac{\beta}{\gamma}\right| \times 100 \%
\tag{4.12}
$$
typora上显示有误,看博客上的;
条件 a 对事件 E 的贡献率为
$$
R C_{a}=1-R C_{b}
\tag{4.13}
$$
可以这么算吗?先算RCa,与1-RCb得到的值不一样吧~~??
按照上述公式,以 QSCAT/NCEP 风场为基础,浮标同步获取的有效波高以及风场数据对同化效果的贡献率分别为 76.9%和 23.1%,比例约为 3.3:1;以 CCMP 风场为基础,浮标同步获取的有效波高以及风场数据对同化效果的贡献率分别为 80.1%和 19.9%,比例约为 4:1. 可见,背景风场精度越高,与海浪数据同步获取的风场在海浪同化中发挥的作用相对于海浪数据在海浪同化中发挥的作用越小。
需要特别指出的是,上面的结论中用到的数据是‘不对等’的。因为,在风场融合中,用到的是 10 个浮标的风速和风向数据,而在海浪同化中用到的则是 1 个浮标的有效波高数据。
貌似1个浮标的有效波高同化更猛呀~~
问题:同化的是44037浮标,和其他4个浮标有什么关系,同化涉及的是场,还是一个点?
4.3.4 融合风场驱动的同化不同浮标数据的结果
从上节的分析中可以得出,以 CCMP_OI 风场作为驱动风场的同化实验所得到的结果最优。本节基于实验 D_44005, D_44011, D_44024 和 D_44037 分析同化不同浮标的有效波高数据对某位置点的影响。表 4.13 列出了相应的同化率, 同化效果见时间序列图 4.15。
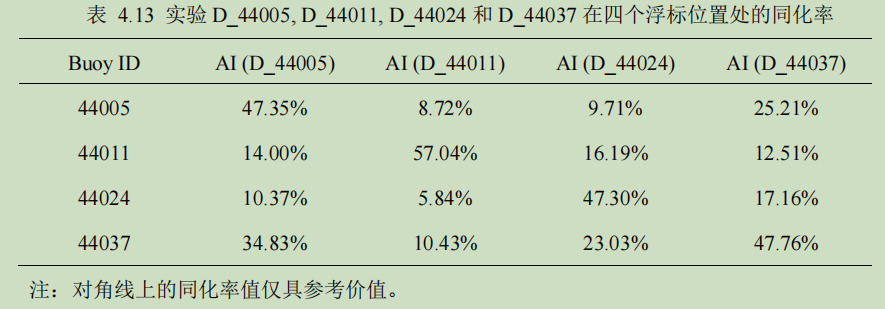
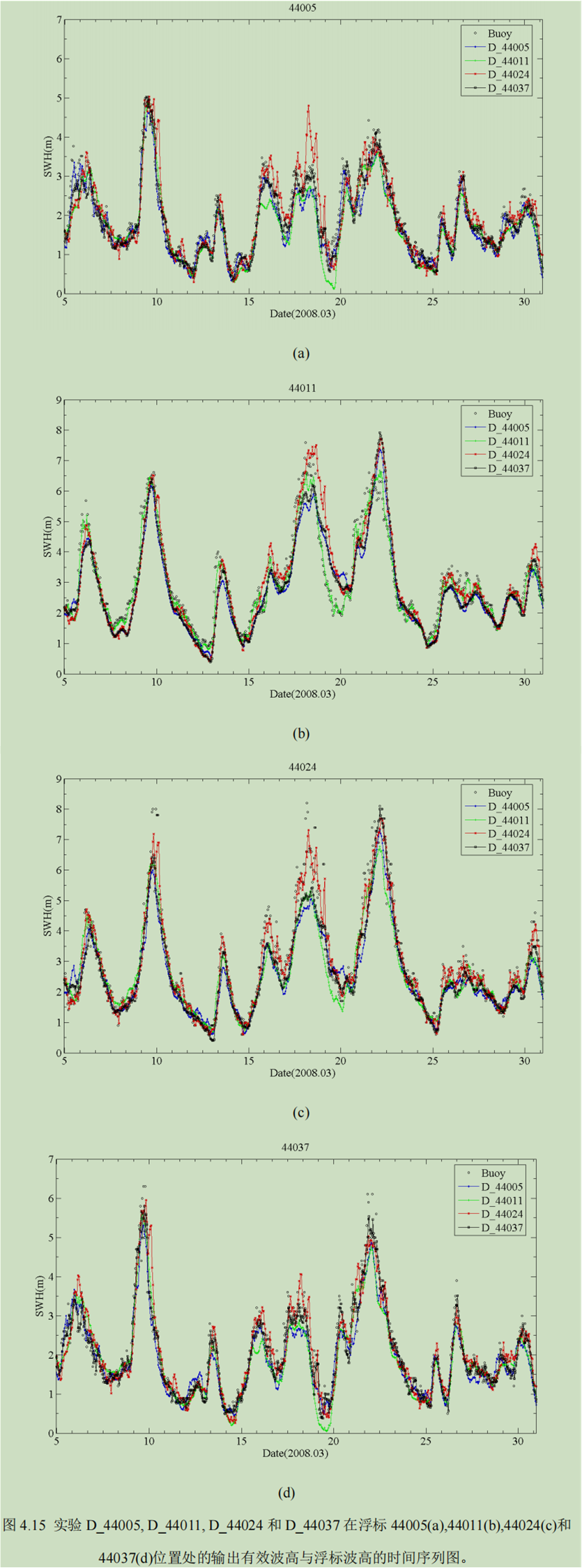
为分析同化率和距离之间的关系,这里给出浮标之间的距离。根据浮标的经纬度计算得出 4 个浮标之间的距离为:
- 浮标 44005 与 44011 之间的距离为 313.21 km;
- 浮标 44005 与 44024 之间的距离为 279.82km;
- 浮标 44005 与 44037 之间的距离为 105.50 km;
- 浮标 44011 与 44024 之间的距离为 145.54 km;
- 浮标 44011 与 44037 之间的距离为 285.11 km;
- 浮标 44024 与 44037 之间的距离为 206.06 km.
同化浮标 44005 的有效波高数据时,在浮标 44037,44024 和 44011 位置处的同化率随着与浮标 44005 的距离的增大而减小,这种情况下的同化率与距离是完全负相关的;同化浮标 44037 的有效波高时在浮标 44005,44024 和 44011 位置处的同化率随着与浮标 44037 的距离的增大而减小,这种情况下的同化率与距离也是完全负相关的;但是,在同化浮标 44011 和 44024 的有效波高时, 其他浮标位置点上的同化率并非完全随着距离的增大而减小,而是存在一定的波动,可能与浮标的数据质量以及岸线的形状有关。可见,同化率并不完全与距离负相关。
4.3.5 不同相关距离尺度的影响
在本章所用的 OI-I 同化方法中,采用第二章中表 2.2 中的公式 5 作为背景误差相关函数,进行浮标有效波高的同化。在诸多的海浪同化的研究中,都对公式中的相关距离尺度 L 进行了研究,针对不同的研究区域给出了最优的相关距离尺度。本节亦在前述的模式设置下,研究不同的相关距离尺度对同化效果的影响,并给出了本实验下的最优相关距离尺度。
本节涉及的实验为表 4.5 中的 D_44037,D_44037_0,D_44037_2 和 D_44037_3,其对应的相关距离尺度依次为 250 km,100 km,500 km 和 700 km。
当相关距离尺度增大时,误差相关函数计算得出的相关系数亦增大,这会增强相同区域内的观测信息的影响。以 CCMP_OI 风场为强迫风场,同化 44037 浮标有效波高数据,根据不同相关距离尺度,得到的浮标 44005、44011、44024 和 44037 位置处的同化效果图见图 4.16.

以 CCMP_OI 风场为强迫风场,同化 44037 浮标有效波高数据,根据不同相关距离尺度,得到的浮标 44005 位置处的统计参数如表 4.14 所示。

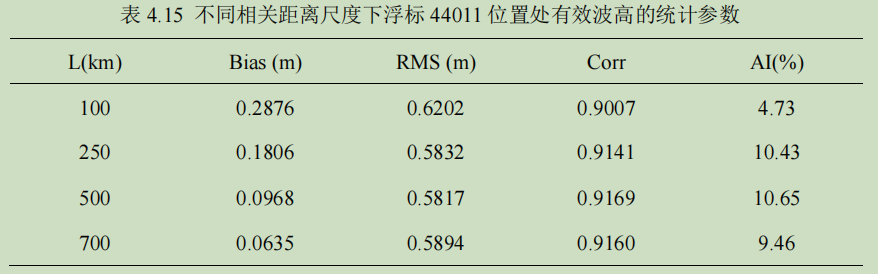
以 CCMP_OI 风场为强迫风场,同化 44037 浮标有效波高数据,根据不同相关距离尺度,得到的浮标 44011 位置处的统计参数如表 4.15 所示。
以 CCMP_OI 风场为强迫风场,同化 44037 浮标有效波高数据,根据不同相关距离尺度,得到的浮标 44024 位置处的统计参数如表 4.16 所示。

以 CCMP_OI 风场为强迫风场,同化 44037 浮标有效波高数据,根据不同相关距离尺度,得到的浮标 44037 位置处的统计参数如表 4.17 所示。
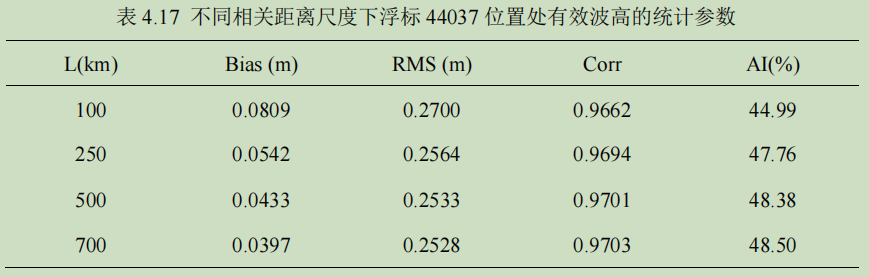
由表 4.14-4.17 可知,相关距离尺度的改变并未大幅度改变相应的统计参数。不同的实验会得到不同的相关距离尺度的最优值,从均方根误差 RMS 上来看,本章所进行的实验的最优相关距离尺度应在 250 km 至 400 km 之间。
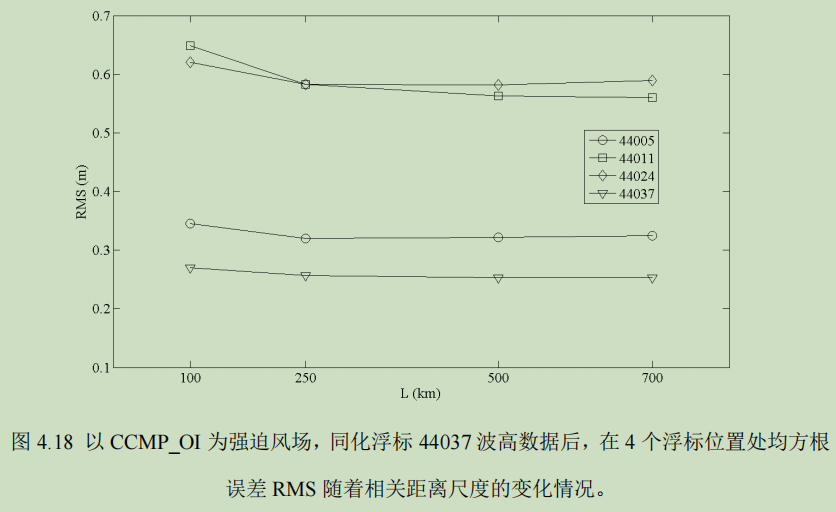
为更清晰地表明上述结论,图 4.17-4.19 进一步给出了以 CCMP_OI 为强迫风场,同化浮标 44037 波高数据后,在 4 个浮标位置处的 Bias、RMS 以及 Corr随着相关距离尺度的变化情况。


4.4 本章小结
本章以 QSCAT/NCEP 和 CCMP 风场为背景风场,融合了浮标风速和风向数据,并以背景风场和融合后的风场作为海浪模式的强迫风场,进行了与浮标风场同步观测的浮标有效波高数据的海浪同化研究,分析考虑同步风场后的海浪模拟和同化效果,分析了同步观测的风和浪在同化中的贡献率,考虑了相关距离尺度对同化效果的影响。主要工作及结论为:
基于 NDBC 浮标的风速和风向数据,评估了 QSCAT/NCEP 和 CCMP 风场, 两种风场数据在量级和空间结构上既有共性又存在差异,精度都比较高。2008 年 3 月 QSCAT/NCEP 风速的 RMS 为 2.93m/s,CCMP 风速的 RMS 为 1.61m/s. 本章中,把 QSCAT/NCEP 风场考虑成精度较低的风场,把 CCMP 风场数据当作高精度风场。
采用最优插值算法把 QSCAT/NCEP 和 CCMP 风场作为背景场,融合了 10 个浮标的风速和风向数据,得到了融合后的更高精度的 NCEP_OI 和 CCMP_OI 风场数据。
最优插值算法如何以场融合点的数据?
根据不同的强迫风场,进行了多组模拟和同化实验,结论主要为:
以 QSCAT/NCEP 作为驱动风场的模式模拟的有效波高 RMS 作为基准值,以 NCEP_OI 作为驱动风场的模式模拟的有效波高 RMS 降低16.30%;以 QSCAT/NCEP 作为驱动风场、同化浮标波高后的模式输出 有效波高 RMS 降低 36.07%;以 NCEP_OI 作为驱动风场、同化浮标波 高后的模式输出有效波高 RMS 降低 43.26%。
以 CCMP 作为驱动风场的模式模拟的有效波高 RMS 作为基准值,以 CCMP_OI 作为驱动风场的模式模拟的有效波高 RMS 降低 16.62%;以 CCMP 作为驱动风场、同化浮标波高后的模式输出有效波高 RMS 降低 33.00%;以 NCEP_OI 作为驱动风场、同化浮标波高后的模式输出有效 波高 RMS 降低 39.22%。
在海浪数据同化中,既融合风场又同化同步观测的海浪数据的同化效果最佳,同步获取的海浪数据与风场对海浪同化效果的贡献率约为 4:1.
背景风场精度越高,与海浪数据同步获取的风场在海浪同化中发挥的作用相对于海浪数据在海浪同化中发挥的作用越小,海浪数据同化能减小海浪模式对强迫风场的高度敏感性。
受数据质量以及岸线形状等因素的影响,同化率并不完全与距离负相关。
可能与一篇文献不太一样;
OI-I 同化方法中的相关距离尺度根据实验的不同而具有不同的最优值, 本章进行的同化实验中的最优相关距离尺度在 250km 至 400km 之间。
下一步:OI的实现,终于来了~~
第五章 基于谱分割策略的海浪谱同化
二维海浪谱中包含诸如有效波高、波周期、传播方向等海浪特征参数信息。海浪有效波高同化只能用海浪的总能量来研究分析海浪谱,研究表明,同化二维海浪谱数据比同化全谱的均值波参数,在物理和实际应用上都有优势。发射于 2002 年的 Envisat 卫星可提供大面积、长时序的二维海浪谱数据,即将由中国的长征火箭发射的中法海洋星 CFOSAT 上将搭载可获取二维海浪谱数据的海 浪波谱仪 SWIM,这些都为二维海浪谱同化提供了数据保障。本章首先用 NDBC 浮标的数据对 Envisat ASAR 波模式的 2 级海浪谱产品进行了比对分析,然后介绍了基于谱分割策略的二维海浪谱同化方法,最后进行了海浪谱的最优插值同化实验。
第六章 结论与展望
学习经历与论文发表情况



